
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5).
(1)在所给的平面直角坐标系中画出它的图象并求一次函数的表达式;
(2)若P点为此一次函数图象上一点,且S△POB=![]() S△AOB,求P点的坐标.
S△AOB,求P点的坐标.

科目:初中数学 来源: 题型:
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
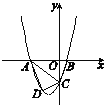
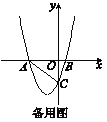
【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() -(k+2)x+2k=0.
-(k+2)x+2k=0.
(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰![]() 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,解答问题:
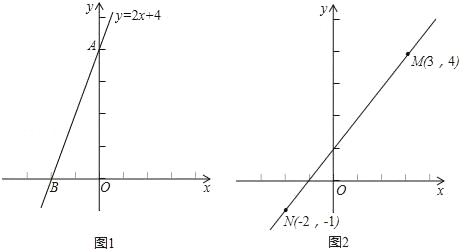
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=100° ,按要求完成画图并解答问题:

(1)画出△ABC的高CE,中线AF,角平分线BD,且AF所在直线交CE于点H,BD与AF相交于点G;
(2)若∠FAB=40°,求∠AFB的度数和∠BCE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com