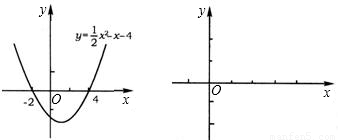
解:(一)x<-2或x>4;-2<x<4;
(二)(Ⅰ)二次函数当1<x<5时,函数值为正,当x<1或x>5时函数值为负,说明二次函数图象经过点(1,0)和(5,0)且开口向下,
即

,
解得p=2,q=-5,
∴二次函数的解析式为y=-x
2+6x-5;
(Ⅱ)(1)解方程组

,
得点A、B的坐标分别为

、(4,3).
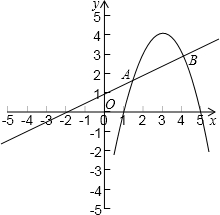
(2)①由题意知
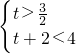
,
∴t的取值范围是

.
②点E的纵坐标为

,点H的纵坐标为-t
2+6t-5,
EH=(-t
2+6t-5)-(

)=

,
点F的纵坐标为

,点G的纵坐标为-t
2+2t+3,
FG=(-t
2+2t+3)-(

)=

,
∵EH∥FG,
∴要使四边形EFGH是平行四边形,只要EH=FG,
即

=

,
解得
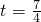
,满足条件

.
∴当
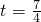
时,四边形EFGH是平行四边形,
此时点E的坐标为

.
分析:(一)看二次函数图象与x轴的交点即可得到答案;
(二)(Ⅰ)根据x的取值范围对应的函数值,可以知道函数图象开口向下和与x轴的交点,由此得到两个等式和一个不等式,解此可得自变量,那么函数解析式可得;
(Ⅱ)(1)把直线的解析式和二次函数的解析式组成一个方程组,解此方程组得A、B的坐标;
(2)①根据A、B的坐标确定t的取值范围;
②求出EH和FG的距离,即可确定四边形EFGH是平行四边形,点E的坐标可求.
点评:此题考查了二次函数与一次函数的综合运用,其中涉及到的知识点有抛物线的顶点、抛物线与x轴和直线的交点,难度较大.

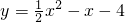 的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.
的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.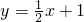 与二次函数的图象交于点A、B.
与二次函数的图象交于点A、B.
 ,
, ,
, 、(4,3).
、(4,3).
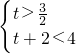 ,
, .
. ,点H的纵坐标为-t2+6t-5,
,点H的纵坐标为-t2+6t-5, )=
)= ,
, ,点G的纵坐标为-t2+2t+3,
,点G的纵坐标为-t2+2t+3, )=
)= ,
, =
= ,
,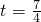 ,满足条件
,满足条件 .
.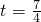 时,四边形EFGH是平行四边形,
时,四边形EFGH是平行四边形, .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案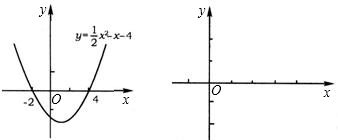
 观察函数图象,回答下列问题:
观察函数图象,回答下列问题: 的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.
的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.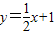 与二次函数的图象交于点A、B.
与二次函数的图象交于点A、B.
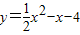 的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.
的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.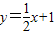 与二次函数的图象交于点A、B.
与二次函数的图象交于点A、B.