
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬µćAĪŖ°ėŌ²OÖ±¾¶MNĖłŌŚÖ±ĻßÉĻŅ»µć£¬ÉäĻßAB“¹Ö±ÓŚMN£¬“¹×ćĪŖA£¬°ėŌ²ČĘMµćĖ³Ź±Õė×Ŗ¶Æ£¬×Ŗ¹żµÄ½Ē¶Č¼Ē×÷a£»Éč°ėŌ²OµÄ°ė¾¶ĪŖR£¬AMµÄ³¤¶ČĪŖm£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
Ģ½¾æ£ŗ£Ø1£©ČōR=2£¬m=1£¬ČēĶ¼1£¬µ±Šż×Ŗ30”揱£¬Ō²ŠÄO”äµ½ÉäĻßABµÄ¾ąĄėŹĒ”” ””£»ČēĶ¼2£¬µ±a=”” ”””揱£¬°ėŌ²OÓėÉäĻßABĻąĒŠ£»
£Ø2£©ČēĶ¼3£¬ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬ĪŖĮĖŹ¹µĆ°ėŌ²O×Ŗ¶Æ30”ć¼“ÄÜÓėÉäĻßABĻąĒŠ£¬ŌŚ±£³ÖĻ߶ĪAM³¤¶Č²»±äµÄĢõ¼žĻĀ£¬µ÷Õū°ė¾¶RµÄ“󊔣¬ĒėÄćĒó³öĀś×ćŅŖĒóµÄR£¬²¢ĖµĆ÷ĄķÓÉ£®
£Ø3£©·¢ĻÖ£ŗ£Ø3£©ČēĶ¼4£¬ŌŚ0”ć£¼¦Į£¼90”揱£¬ĪŖĮĖ¶ŌČĪŅāŠż×Ŗ½Ē¶¼±£Ö¤°ėŌ²OÓėÉäĻßABÄܹ»ĻąĒŠ£¬Š”Ć÷Ģ½¾æĮĖcos¦ĮÓėR”¢mĮ½øöĮæµÄ¹ŲĻµ£¬ĒėÄć°ļÖśĖūÖ±½ÓŠ“³öÕāøö¹ŲĻµ£»
cos¦Į=”” ””£ØÓĆŗ¬ÓŠR”¢mµÄ“śŹżŹ½±ķŹ¾£©
ĶŲÕ¹£ŗ£Ø4£©ČēĶ¼5£¬ČōR=m£¬µ±°ėŌ²»”ĻßÓėÉäĻßABÓŠĮ½øö½»µćŹ±£¬¦ĮµÄȔֵ·¶Ī§ŹĒ”” ””£¬²¢Ēó³öŌŚÕāøö±ä»Æ¹ż³ĢÖŠŅõÓ°²æ·Ö£Ø¹ŠĪ£©Ć껿µÄ×ī“óÖµ£ØÓĆm±ķŹ¾£©

”¾“š°ø”æ£Ø1£©![]() +1£»60”ć£»£Ø2£©4+2
+1£»60”ć£»£Ø2£©4+2![]() £»£Ø3£©
£»£Ø3£©![]() £»£Ø4£©
£»£Ø4£©![]() m2£®
m2£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬×÷O”äE”ĶABÓŚE£¬MF”ĶO”äEÓŚF£®ŌņĖıߊĪAMFEŹĒ¾ŲŠĪ£¬EF=AM=1£®ČēĶ¼2ÖŠ£¬ÉčĒŠµćĪŖF£¬Į¬½ÓO”äF£¬×÷O”äE”ĶOAÓŚE£¬ŌņĖıߊĪO”äEAFŹĒ¾ŲŠĪ£¬ŌŚRt”÷O”äEMÖŠ£¬ÓÉsin¦Į=![]() £¬ĶĘ³ö¦Į=60”ć£®
£¬ĶĘ³ö¦Į=60”ć£®
£Ø2£©ÉčĒŠµćĪŖP£¬Į¬½ÓO”äP£¬×÷MQ”ĶO”äP£¬ŌņĖıߊĪAPQMŹĒ¾ŲŠĪ£®ĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£®
£Ø3£©ÉčĒŠµćĪŖP£¬Į¬½ÓO”äP£¬×÷MQ”ĶO”äP£¬ŌņĖıߊĪAPQMŹĒ¾ŲŠĪ£®ĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā”¢
£Ø4£©µ±°ėŌ²ÓėÉäĻßABĻąĒŠŹ±£¬Ö®ŗóæŖŹ¼³öĻÖĮ½øö½»µć£¬“ĖŹ±¦Į=90”ć£»µ±N”äĀäŌŚABÉĻŹ±£¬ĪŖ°ėŌ²ÓėABÓŠĮ½øö½»µćµÄ×īŗóŹ±æĢ£¬“ĖŹ±”ßMN”ä=2AM£¬ĖłŅŌ”ĻAMN”ä=60”ć£¬ĖłŅŌ£¬¦Į=120”ćŅņ“Ė£¬µ±°ėŌ²»”ĻßÓėÉäĻßABÓŠĮ½øö½»µćŹ±£¬¦ĮµÄȔֵ·¶Ī§ŹĒ£ŗ90”ć£¼¦Į”Ü120”ć£®µ±N”äĀäŌŚABÉĻŹ±£¬ŅõÓ°²æ·ÖĆ껿×ī“ó£¬Ēó³ö“ĖŹ±µÄĆ껿¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬×÷O”äE”ĶABÓŚE£¬MF”ĶO”äEÓŚF£®ŌņĖıߊĪAMFEŹĒ¾ŲŠĪ£¬EF=AM=1£®Ļė°ģ·ØĒó³öO”äEµÄ³¤¼“æÉ£®
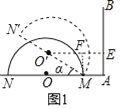
ŌŚRt”÷MFO”äÖŠ£¬”ß”ĻMO![]() F=30”ć£¬MO”ä=2£¬
F=30”ć£¬MO”ä=2£¬
”ąO”äF=O”äMcos30”ć=![]() £¬O”äE=
£¬O”äE=![]() +1£¬
+1£¬
”ąµćO”äµ½ABµÄ¾ąĄėĪŖ![]() +1£®
+1£®
ČēĶ¼2ÖŠ£¬ÉčĒŠµćĪŖF£¬Į¬½ÓO”äF£¬×÷O”äE”ĶOAÓŚE£¬ŌņĖıߊĪO”äEAFŹĒ¾ŲŠĪ£¬

”ąAE=O”äF=2£¬
”ßAM=1£¬
”ąEM=1£¬
ŌŚRt”÷O”äEMÖŠ£¬sin¦Į=![]() £¬
£¬
”ą¦Į=60”ć
¹Ź“š°øĪŖ![]() +1£¬60”ć£®
+1£¬60”ć£®
£Ø2£©ÉčĒŠµćĪŖP£¬Į¬½ÓO”äP£¬×÷MQ”ĶO”äP£¬ŌņĖıߊĪAPQMŹĒ¾ŲŠĪ£®
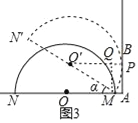
”ßO”äP=R£¬
”ąR=![]() R+1£¬
R+1£¬
”ąR=4+2![]() £®
£®
£Ø3£©ÉčĒŠµćĪŖP£¬Į¬½ÓO”äP£¬×÷MQ”ĶO”äP£¬ŌņĖıߊĪAPQMŹĒ¾ŲŠĪ£®
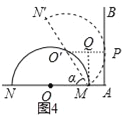
ŌŚRt”÷O”äQMÖŠ£¬O”äQ=Rcos¦Į£¬QP=m£¬
”ßO”äP=R£¬
”ąRcos¦Į+m=R£¬
”ącos¦Į=![]() £®
£®
¹Ź“š°øĪŖ![]() £®
£®
£Ø4£©ČēĶ¼5ÖŠ£¬
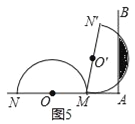
µ±°ėŌ²ÓėÉäĻßABĻąĒŠŹ±£¬Ö®ŗóæŖŹ¼³öĻÖĮ½øö½»µć£¬“ĖŹ±¦Į=90”ć£»µ±N”äĀäŌŚABÉĻŹ±£¬ĪŖ°ėŌ²ÓėABÓŠĮ½øö½»µćµÄ×īŗóŹ±æĢ£¬“ĖŹ±”ßMN”ä=2AM£¬ĖłŅŌ”ĻAMN”ä=60”ć£¬ĖłŅŌ£¬¦Į=120”ćŅņ“Ė£¬µ±°ėŌ²»”ĻßÓėÉäĻßABÓŠĮ½øö½»µćŹ±£¬¦ĮµÄȔֵ·¶Ī§ŹĒ£ŗ90”ć£¼¦Į”Ü120”ć
¹Ź“š°øĪŖ90”ć£¼¦Į”Ü120”ć£»
µ±N”äĀäŌŚABÉĻŹ±£¬ŅõÓ°²æ·ÖĆ껿×ī“ó£¬
ĖłŅŌSØT![]() ©
©![]()
![]() m
m![]() m=
m=![]() m2£®
m2£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ”ĒųÓŠĮ½¶Ī³¤¶ČĻąµČµÄµĄĀ·ŠčÓ²»Æ£¬ĻÖ·Ö±šÓɼה¢ŅŅĮ½øö¹¤³Ģ¶ÓĶ¬Ź±æŖŹ¼Ź©¹¤£®ČēĶ¼µÄĻ߶ĪŗĶÕŪĻߏĒĮ½¶ÓĒ°6ĢģÓ²»ÆµÄµĄĀ·³¤y¼×”¢yŅŅ£ØĆ×£©ÓėŹ©¹¤Ź±¼äx£ØĢģ£©Ö®¼äµÄŗÆŹżĶ¼Ļó
øł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ö±½ÓŠ“³öy¼×”¢yŅŅ£ØĆ×£©Óėx£ØĢģ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
¢Łµ±0£¼x”Ü6Ź±£¬y¼×£½£»
¢Śµ±0£¼x”Ü2Ź±£¬yŅŅ£½£»µ±2£¼x”Ü6Ź±£¬yŅŅ£½£»
£Ø2£©ĒóĶ¼ÖŠµćMµÄ×ų±ź£¬²¢ĖµĆ÷MµÄŗį”¢×Ż×ų±ź±ķŹ¾µÄŹµ¼ŹŅāŅ壻
£Ø3£©Ź©¹¤¹ż³ĢÖŠ£¬¼×¶ÓµÄŹ©¹¤ĖŁ¶ČŹ¼ÖÕ²»±ä£¬¶ųŅŅ¶ÓŌŚŹ©¹¤6Ģģŗó£¬ĆæĢģµÄŹ©¹¤ĖŁ¶ČĢįøßµ½120Ć×£ÆĢģ£¬Ō¤¼ĘĮ½¶Ó½«Ķ¬Ź±Ķź³ÉČĪĪń£®Į½¶Ó»¹ŠčŅŖ¶ąÉŁĢģĶź³ÉČĪĪń£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖP1£Ø©2£¬y1£©£¬P2£Ø©1£¬y2£©ŹĒÕż±ČĄżŗÆŹży=©xµÄĶ¼ĻóÉĻµÄĮ½µć£¬Ōņy1 y2£ØĢī”°£¾”±»ņ”°£¼”±»ņ”°=”±£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻߵĶ„µćĪŖA£Ø0£¬1£©£¬¾ŲŠĪCDEFµÄ¶„µćC”¢FŌŚÅ×ĪļĻßÉĻ£¬µćD”¢EŌŚxÖįÉĻ£¬CF½»yÖįÓŚµćB£Ø0£¬2£©£¬ĒŅ¾ŲŠĪĘäĆ껿ĪŖ8£¬“ĖÅ×ĪļĻߵĽāĪöŹ½£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūŅ»øö½ĒŹĒ50”ć£¬ÄĒĆ“ĖüµÄÓą½ĒµÄ¶ČŹżŹĒ(””””)£®
A.40”ćB.50”ćC.100”ćD.130”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚRt”÷ABCÖŠ£¬AB£½AC£¬”ĻBAC=90”ć£¬OĪŖBCµÄÖŠµć”£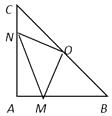
£Ø1£©Š“³öµćOµ½”÷ABCµÄČżøö¶„µćA”¢B”¢CµÄ¾ąĄėµÄ“󊔹ŲĻµ²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©Čē¹ūµćM”¢N·Ö±šŌŚĻ߶ĪAB”¢ACÉĻŅĘ¶Æ£¬ŌŚŅʶÆÖŠ±£³ÖAN£½BM£¬ĒėÅŠ¶Ļ”÷OMNµÄŠĪד£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōµćP£Øx£¬y£©ŌŚµŚČżĻóĻŽ£¬ĒŅµćPµ½xÖįµÄ¾ąĄėĪŖ3£¬µ½yÖįµÄ¾ąĄėĪŖ2£¬ŌņµćPµÄ×ų±źŹĒ£Ø £©
A.£Ø©2£¬©3£©
B.£Ø©2£¬3£©
C.£Ø2£¬©3£©
D.£Ø2£¬3£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖŠ¹śŗ½æÕÄø½¢”°ĮÉÄžŗÅ”±µÄĀśŌŲÅÅĖ®ĮæĪŖ67500¶Ö£®½«Źż67500ÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾ĪŖ£Ø £©
A.0.675”Į105
B.6.75”Į104
C.67.5”Į103
D.675”Į102
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com