
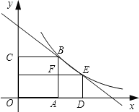
【题目】如图,正方形![]() ,
,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 在坐标轴上,点
在坐标轴上,点![]() 在
在![]() 上,点
上,点![]() ,
,![]() 在双曲线
在双曲线![]() 上,若点
上,若点![]() 的横坐标为
的横坐标为![]() ,则直线
,则直线![]() 的函数解析式为________.
的函数解析式为________.
【答案】![]()
【解析】
由点B的横坐标为2,根据图形得到正方形OABC的边长和点B的坐标,设出正方形ADEF的边长为a,由点B和E在同一个双曲线上,列出关于a的方程,求出方程的解得到a的值,进而得到点E的坐标,设出直线BE的解析式为y=kx+b,把点B和E的坐标代入即可求出k和b的值,确定出直线BE的解析式.
设正方形ADEF的边长为a,由点B的横坐标为2,
得到正方形OABC的边长为2,即B坐标为(2,2),
则点E的坐标为(a+2,a)(a>0),又点B和E在同一个双曲线上,
∴a(a+2)=4,即(a+1)2=5,解得:a=![]() -1或a=-
-1或a=-![]() -1(舍去),
-1(舍去),
∴点E坐标为(![]() +1,
+1,![]() -1),
-1),
设直线BE的函数解析式为y=kx+b,将点E和B的坐标代入得:
![]() ,解得
,解得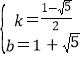 ,
,
∴直线BE的解析式为y=![]() x+1+
x+1+![]() .
.
故答案为:y=![]() x+1+
x+1+![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】田忌赛马是一个为人熟知的故事.传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出-匹,每匹马赛一次,赢得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强.
(1)如果齐王将马按下中上的顺序出阵比赛,那么田忌的马如何出阵才能获胜?
(2)如果齐王将马按下中上的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车油箱中的余油量![]() (升)随汽车行驶的时间
(升)随汽车行驶的时间![]() (时)的变化而变化,
(时)的变化而变化,![]() 与
与![]() 之间的关系为
之间的关系为![]() ,其中
,其中![]() 是油箱中原有的油的升数,若这辆汽车油箱中原有油60升.
是油箱中原有的油的升数,若这辆汽车油箱中原有油60升.
(1)用表格表示行驶1到5小时过程中这辆汽车油箱中余油量与行驶时间![]() 的关系,填写下表:
的关系,填写下表:
行驶时间(时) | 1 | 2 | 3 | 4 | 5 |
余油量(升) |
(2)这辆车最多可行驶多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求CE1的长;
(3)连接PA,△PAB面积的最大值为 .(直接填写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某陶瓷公司招工广告称:“本公司工人工作时间:每天工作![]() 小时,每月工作
小时,每月工作![]() 天;待遇:工人按计件付工资,每月另加生活费
天;待遇:工人按计件付工资,每月另加生活费![]() 元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
元,按月结算…”.该公司只生产甲、乙两种陶瓷,工人小王记录了如下一些数据:
甲种陶瓷 (单位:个) | 乙种陶瓷 (单位:个) | 总时间 (单位:分钟) | 计件工资 (单位:元) |
|
|
|
|
|
|
|
|
(1)设生产每个甲种陶瓷所需的时间为![]() 分钟,用含有
分钟,用含有![]() 的代数式表示生产每个乙种陶瓷所需的时间;
的代数式表示生产每个乙种陶瓷所需的时间;
(2)设小王工人小王某月(工作![]() 天)生产甲种陶瓷
天)生产甲种陶瓷![]() 个,乙种陶瓷
个,乙种陶瓷![]() 个,
个,
①试求![]() 与
与![]() 的函数关系式;(不需写出自变量
的函数关系式;(不需写出自变量![]() 的取值范围)
的取值范围)
②根据市场调查,每个工人每月生产甲种陶瓷的数量不少于乙种陶瓷数量的![]() 倍,且生产每个乙种陶瓷的计件工资可提高
倍,且生产每个乙种陶瓷的计件工资可提高![]() 元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资
元,甲种陶瓷计件工资也有提高的空间.若小王的工作效率不变,甲种陶瓷计件工资至少要提高多少元,小王的月工资(计件工资+福利工资![]() 月工资)才能领到
月工资)才能领到![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
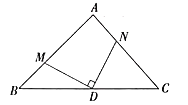
【题目】综合与实践
已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)如图:过![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() .求证:
.求证:![]() .
.
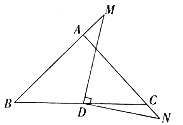
(2)如图,若![]() ,分别与
,分别与![]() 、
、![]() 的延长线交于点
的延长线交于点![]() 、
、![]() ,此时(1)中的结论还成立吗?若成立,请说明理由,若不成立,请举例说明.
,此时(1)中的结论还成立吗?若成立,请说明理由,若不成立,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
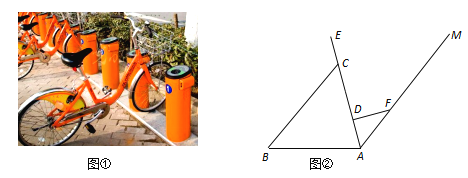
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com