
【题目】如图,在Rt△ABC中,AC=8cm,BC=6cm,P点在BC上,从B点到C点运动(不包括 C点),点 P运动的速度为1cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2cm/s,若点 P、Q 分别从B、C 同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当 t 为何值时,P、Q 两点的距离为 4![]() cm?
cm?
(2)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?

【答案】(1) 2或![]() ;(2) 3秒,15cm2.
;(2) 3秒,15cm2.
【解析】
(1)根据勾股定理PC2+CQ2=PQ2,便可求出经过2或![]() s后,P、Q两点的距离为4
s后,P、Q两点的距离为4![]() cm;(2)根据三角形的面积公式S△PCQ=
cm;(2)根据三角形的面积公式S△PCQ=![]() ×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
:(1)∵在Rt△ABC中,AC=8cm,BC=6cm,
∴AB=10cm,
设经过ts后,P、Q两点的距离为4![]() cm,
cm,
ts后,PC=6-t cm,CQ=2t cm,
根据勾股定理可知PC2+CQ2=PQ2,
代入数据(6-t)2+(2t)2=(4![]() )2;
)2;
解得t=2或t=![]() ,
,
故t为2或![]() 时,P、Q两点的距离为4
时,P、Q两点的距离为4![]() cm;
cm;
(2)设经过ts后,△PCQ的面积最大,则此时四边形BPQA的面积最小,
ts后,PC=6-tcm,CQ=2t cm,
S△PCQ=![]() ×PC×CQ=
×PC×CQ=![]() ×(6-t)×2t=-t2+6t
×(6-t)×2t=-t2+6t
当t=-![]() 时,即t=3s时,△PCQ的面积最大,
时,即t=3s时,△PCQ的面积最大,
即S△PCQ=![]()
×PC×CQ=![]() ×(6-3)×6=9(cm2),
×(6-3)×6=9(cm2),
∴四边形BPQA的面积最小值为:S△ABC-S△PCQ最大=![]() ×6×8-9=15(cm2),
×6×8-9=15(cm2),
当点P运动3秒时,四边形BPQA的面积最小为:15cm2.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
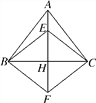
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
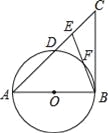
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
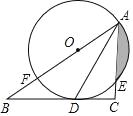
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学概念)
若等边三角形的三个顶点D、E、F分别在△ABC的三条边上,我们称等边三角形DEF是△ABC的内接正三角形.
(概念辨析)
(1)下列图中△DEF均为等边三角形,则满足△DEF是△ABC的内接正三角形的是 .
A.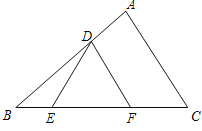 B.
B.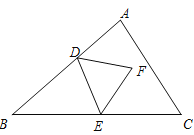
C.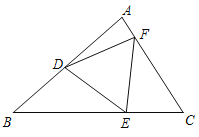
(操作验证)
(2)如图①.在△ABC中,∠B=60°,D为边AB上一定点(BC>BD),DE=DB,EM平分∠DEC,交边AC于点M,△DME的外接圆与边BC的另一个交点为N.
求证:△DMN是△ABC的内接正三角形.
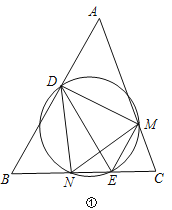
(知识应用)
(3)如图②.在△ABC中,∠B=60°,∠A=45°,BC=2,D是边AB上的动点,若边BC上存在一点E,使得以DE为边的等边三角形DEF是△ABC的内接正三角形.设△DEF的外接圆⊙O与边BC的另一个交点为K,则DK的最大值为 ,最小值为 .
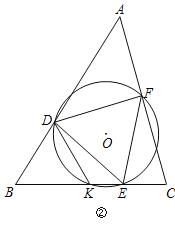
查看答案和解析>>
科目:初中数学 来源: 题型:
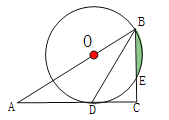
【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com