
【题目】如图,△ABC 中,BO 平分∠ABC,CO 平分∠ACB,MN 经过点 O,与 AB、AC 相交于点 M、N,且 MN∥BC,那么下列说法中:①∠MOB=∠MBO②△AMN 的周长等于 AB+AC;③∠A=2∠BOC﹣180°;④连接 AO,则![]() :
:![]() :
:![]() =AB:AC:BC;正确的有( )
=AB:AC:BC;正确的有( )
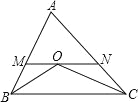
A. ①②④ B. ①②③ C. ①③④ D. ①②③④
【答案】D
【解析】
根据角平分线的定义可得∠ABO=∠CBO,根据两直线平行,内错角相等可得∠CBO=∠BOM,从而得到∠ABO=∠BOM,再根据等角对等边可得BM=OM,同理可得CN=ON,然后即可求出ΔAMN的周长=AB+AC,由ΔABC、ΔBOC内角和为180![]() ,及BO 平分∠ABC,CO 平分∠ACB可得∠A=2∠BOC﹣180
,及BO 平分∠ABC,CO 平分∠ACB可得∠A=2∠BOC﹣180![]() ,可得点O为ΔABC的内心,可得
,可得点O为ΔABC的内心,可得![]() :
:![]() :
:![]() =AB:AC:BC,可得答案.
=AB:AC:BC,可得答案.
解:![]() BO 平分∠ABC,CO 平分∠ACB,
BO 平分∠ABC,CO 平分∠ACB,![]() ∠ABO=∠CBO
∠ABO=∠CBO
![]() MN∥BC,
MN∥BC,![]() ∠CBO=∠BOM,
∠CBO=∠BOM,![]() ∠MOB=∠MBO,故①正确;
∠MOB=∠MBO,故①正确;
![]() BM=OM,同理CN=ON,
BM=OM,同理CN=ON,![]() △AMN 的周长等于 AB+AC,故②正确;
△AMN 的周长等于 AB+AC,故②正确;
![]() 由ΔABC、ΔBOC内角和为180
由ΔABC、ΔBOC内角和为180![]()
![]() ∠A+∠ABC+∠ACB=180
∠A+∠ABC+∠ACB=180![]() ,即:∠A+2(∠OBC+∠OCB)=180
,即:∠A+2(∠OBC+∠OCB)=180![]() ,
,
![]() ∠OBC+∠OCB+∠BOC=180
∠OBC+∠OCB+∠BOC=180![]() ,即∠OBC+∠OCB=180
,即∠OBC+∠OCB=180![]() -∠BOC,
-∠BOC,
可得:∠A=2∠BOC﹣180°,故③正确;
由题意得:点O为ΔABC的内心,设内切圆半径为r,可得![]() :
:![]() :
:![]() =
=![]() AB:
AB:![]() AC:
AC:![]() BC= AB:AC:BC,故④正确
BC= AB:AC:BC,故④正确
故选D.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,抛物线y=mx2﹣2m2x+2交y轴于A点,交直线x=4于B点.
(1)抛物线的对称轴为x=(用含m的代数式表示);
(2)若AB∥x轴,求抛物线的表达式;
(3)记抛物线在A,B之间的部分为图象G(包含A,B两点),若对于图象G上任意一点P(xp , yp),yp≤2,求m的取值范围. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-![]() .
.
∴x=-![]() 是方程2x3-x2+m=0的解.
是方程2x3-x2+m=0的解.
∴2×(-![]() )3-(-
)3-(-![]() )2+m=0,即-
)2+m=0,即-![]() -
-![]() +m=0.
+m=0.
∴m=![]() .
.
请你模仿上面的方法尝试解决下面的问题:
若多项式x4+mx3+nx-16分解因式的结果中有因式(x-1)和(x-2),求实数m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD 和 BE 是△ABC 的两条高,∠BCD=45°,BF=FC,BE与 DF、DC分别交于点 G、H,∠ACD=∠CBE.
(1)证明:AB=BC;
(2)判断 BH 与 AE 之间的数量关系,并证明你的结论;
(3)结合已知条件,观察图形,你还能发现什么结论?请写出两个(不与前面结论相同).
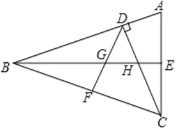
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
(1)请你在所给的平面直角坐标系中,画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)将(1)中得到的![]() 向下移动4个单位得到
向下移动4个单位得到![]() ,画出
,画出![]() ;
;
(3)在![]() 中有一点
中有一点![]() ,直接写出经过以上两次图形变换后
,直接写出经过以上两次图形变换后![]() 中对应点
中对应点![]() 的坐标.
的坐标.
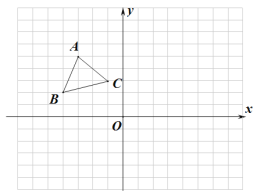
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com