
 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G,连接GF,下列结论中正确的是①②③.(填序号)
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G,连接GF,下列结论中正确的是①②③.(填序号) 分析 根据正方形的性质、菱形的判定、等腰直角三角形的性质,相似三角形的性质,勾股定理一一判断即可.
解答 解: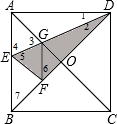 ∵四边形ABCD为正方形,
∵四边形ABCD为正方形,
∴∠AOB=90°,∠BAO=∠OAD=∠ODA=45°,
∵折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的F重合,
∴∠1=∠2=$\frac{1}{2}$∠ODA=22.5°,EA=EF,∠4=∠5,∠EFD=∠EAD=90°,
∴∠3=∠GAD+∠1=45°+22.5°=67.5°,即∠AGE=67.5°;故①正确,
∵∠4=90°-∠1=67.5°,
∴∠3=∠4=∠5,
∴AE=AG=EF,AG∥EF,
∴四边形AEFG为菱形;故②正确,
∴GF∥AB,EF=GF,
∴∠6=∠7=45°,
∴△BEF和△OGF都是等腰直角三角形,
∴BE=$\sqrt{2}$EF,GF=$\sqrt{2}$OF,
∴BE=$\sqrt{2}$•$\sqrt{2}$OF=2OF;故③正确,
设OF=a,则GF=$\sqrt{2}$a,BF=$\sqrt{2}$a,
∴OB=( $\sqrt{2}$+1)a,
∴OD=( $\sqrt{2}$+1)a,DF=DO+OF=(2+$\sqrt{2}$)a,
∵∠DOG=∠DFE=90°,
∴△DOG∽△DFE,
∴$\frac{{S}_{△DOG}}{{S}_{△DFE}}$=( $\frac{DO}{DF}$)2=[$\frac{(\sqrt{2}+1)a}{(2+\sqrt{2})a}$]2=$\frac{1}{2}$,
∴S△DOG:S四边形OGEF=1:1.故④错误.
故答案为①②③
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形和等腰直角三角形的性质.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x=$\frac{y-2}{3}$ | B. | x=$\frac{2-y}{3}$ | C. | y=3x-2 | D. | y=2-3x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在15×15的正方形网格中建立平面直角坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在15×15的正方形网格中建立平面直角坐标系,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com