
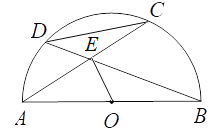
【题目】如图,以AB为直径的半圆O内有一条弦AC,点E是弦AC的中点,连接BE,并延长交半圆O于点D,若OB=2,OE=1,则∠CDE的度数是_______________.
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.
,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.
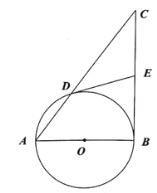
(1)求证:DE是![]() 的切线;
的切线;
(2)设![]() 的半径为r,证明
的半径为r,证明![]() ;
;
(3)若![]() ,求AD之长.
,求AD之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD,过点A作BC的垂线,垂足为点E,且满足AE=EC,过点C作AB的垂线,垂足为点F,交AE于点G,连接BG.

(1)如图1,若AC=![]() ,CD=4,求BC的长度;
,CD=4,求BC的长度;
(2)如图2取AC上一点Q,连接EQ,在△QEC内取一点,连接QH,EH,过点H作AC的垂线,垂足为点P,若QH=EH,∠QEH=45°.求证:AQ=2HP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2﹣4ax﹣5的开口向上.
(1)当a=1时,求抛物线与x轴的交点坐标;
(2)试说明抛物线C1一定经过两个定点,并求出这两个定点的坐标;
(3)将抛物线C1沿(2)所求的两个定点所在直线翻折,得到抛物线C2,
①写出抛物线C2的表达式;
②当抛物线C2的顶点到x轴的距离为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
查看答案和解析>>
科目:初中数学 来源: 题型:
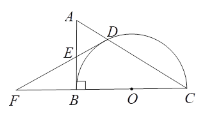
【题目】如图,在Rt△ABC中,∠ABC=90o,以BC为直径的半圆⊙O交AC于点D,点E是AB的中点,连接DE并延长,交CB延长线于点F.
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)若CF=8,DF=4,求⊙O的半径和AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1:y=2(x﹣3)2+1和抛物线y2:y=﹣2x2﹣8x﹣3,若无论k取何值,直线y=kx+km+n被两条抛物线所截的两条线段都保持相等,则m=_____,n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)从中任取一张,求取到偶数的概率.
(2)甲、乙两人进行摸牌游戏.
①甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
②若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com