练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
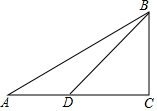
    20．如图，在Rt△ABC中，∠A=30°，CD=CB，则∠ABD的度数是（　　）
    A．15°B．20°C．30°D．60°

    分析 根据直角三角形两锐角互余求出∠ABC，再根据等腰直角三角形两底角相等求出∠CBD，然后根据∠ABD=∠ABC-∠CBD，代入数据进行计算即可得解．

    解答 解：∵∠A=90°，∠A=30°，
    ∴∠ABC=90°-∠A=90°-30°=60°，
    ∵CD=CB，
    ∴∠CBD=45°，
    ∴∠ABD=∠ABC-∠CBD
    =60°-45°
    =15°．
    故选：A．

    点评 本题考查了等腰三角形两底角相等的性质，直角三角形两锐角互余的性质，熟记性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．《九章算术》是我国古代内容极为丰富的数学名著，书中有这样一个问题：“今有勾八步，股十五步，问勾中容圆，径几何？”其意思是：“如图，今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆形（内切圆）直径是多少？”此问题中，该内切圆的直径是（　　）
    A．5步B．6步C．8步D．10步

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．抛物线的y=（x-3）2-2的最小值为-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．代数式2a+1与1-3a互为相反数，则a=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．代数式$\sqrt{x-4}$中x的取值范围是（　　）
    A．x＞4B．x≠4C．x≤4D．x≥4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

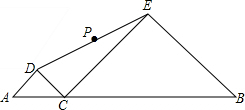    2．如图，线段AB长为6，点C是线段AB上一动点（不与A，B重合）分别以AC和BC为斜边，在AB的同侧作等腰直角三角形△ADC，△CEB，点P是DE的中点，当点C从距离A点1处沿AB向右运动至距离B点1处时，点P运动的路径长是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．化简与计算：
    （1）$\sqrt{12}-{（2014-\sqrt{5}）^0}+|{\sqrt{3}-1}$|
    （2）$（\sqrt{2}-\sqrt{6}）（1+\sqrt{3}）$
    （3）已知m=1+$\sqrt{2}$，n=1-$\sqrt{2}$，求代数式$\sqrt{{m}^{2}+{n}^{2}-3mn}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．化简（x+y）-1的结果是（　　）
    A．x-1+y-1B．$\frac{1}{xy}$C．$\frac{1}{x}$+$\frac{1}{y}$D．$\frac{1}{x+y}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．计算：-3×2+（-2）2-3的结果是-5．

    查看答案和解析>>

    同步练习册答案