
分析 (1)根据$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,可得答案;
(2)根据$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,可得答案.
解答 解:(1)1×(-2)-3×(-3)=7,
故答案为:7,
(2)因为$\left|\begin{array}{l}x+8\\ 3\end{array}\right.$$\left.\begin{array}{l}x-1\\ 2\end{array}\right|$=0
所以2(x+8)-3(x-1)=0
解得x=19.
点评 本题考查了解一元一次方程,利用$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc得出方程是解题关键.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
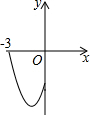 在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)
在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
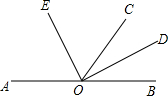 如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com