
【题目】有理数a、b在数轴上的对应点如图所示
![]()
(1) 填空:(填“<”、“>”或“=”)
a_________0;b_________0;|a+b|_________|a|+|b|
(2) 用“<”将a、b、-b、![]() 、0连接起来
、0连接起来
(3) 化简:|a+b|-|b+1|-|a-1|=______________
【答案】(1)>,<,<;(2)b<![]() <0< a<-b;(3)0.
<0< a<-b;(3)0.
【解析】
(1)观察数轴,根据a、b在数轴上的位置即可解答;(2)把a、b、-b、![]() 、0在数轴上表示出来,根据他们在数轴上的位置即可解答;(3)先确定a+b<0,b+1<0,a-1<0,再根据绝对值的性质即可解答.
、0在数轴上表示出来,根据他们在数轴上的位置即可解答;(3)先确定a+b<0,b+1<0,a-1<0,再根据绝对值的性质即可解答.
(1)观察数轴可得,a>0,b<0,|a+b|<|a|+|b| .
故答案为:>,<,<;
(2)把a、b、-b、![]() 、0在数轴上表示如下,
、0在数轴上表示如下,
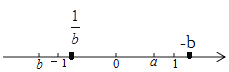
∴b<![]() <0< a<-b;
<0< a<-b;
(3)观察数轴可得,0<a<1;b<-1,
∴a+b<0,b+1<0,a-1<0,
∴|a+b|-|b+1|-|a-1|=-(a+b)-(-b-1)-(1-a)=-a-b+b+1-1+a=0.


科目:初中数学 来源: 题型:
【题目】观察下面三行数
①2,-4,8,-16,32,-64,......;
②4,-2,10,-14,34,-62,......;
③-1,2,-4,8,-16,32,......;
取每一行的第n个数,依次记为a,b,c. 如上图,当n=2时,x=-4,y=-2,z=2.
(1)当n=7时,请直接写出x、y、z的值,并求这三个数中最大的数与最小的数的差;
(2)已知n为偶数,且x、y、z这三个数中最大的数与最小的数的差为384,求n的值;
(3)若m=x+y+z,则x、y、z这三个数中最大的数与最小的数的差为______(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.

(1)判断△OBC的形状,并证明你的结论
(2)求BC的长
(3)求⊙O的半径OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A:国学诵读”,“B:演讲”,“C:课本剧”,“D:书法”.每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如图所示:

(1) 此次一共抽取 名学生进行统计调查;扇形统计图中,活动D所占圆心角为 °;
(2) 请补全条形统计图;
(3) 学校共有720名学生希望参加活动A,试估算该校共有多少名学生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,连接对角线AC.
(1)在边AD上确定一点E,使EA=EC;在边BC上确定一点F,使FA=FC;(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AF,CE.求证:四边形AFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过第一、二、三象限,且与反比例函数图象相交于
的图象经过第一、二、三象限,且与反比例函数图象相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
, ![]() .且点
.且点![]() 横坐标是点
横坐标是点![]() 纵坐标的2倍.
纵坐标的2倍.
(1)求反比例函数的解析式;
(2)设点![]() 横坐标为
横坐标为![]() ,
, ![]() 面积为
面积为![]() ,
,
求![]() 与
与![]() 的函数关系式,并求出自变量的取值范围.
的函数关系式,并求出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com