
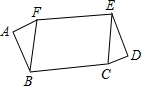
 如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC.
如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC. 分析 根据一组对边平行且相等的四边形是平行四边形可得四边形BCEF是平行四边形,根据平行四边形的对边相等可得BF=CE,再利用“角角边”证明△ABF和△DEC全等,根据全等三角形对应边相等可得AF=DC.
解答 证明:∵BC=EF,BC∥EF,
∴四边形BCEF是平行四边形,
∴BF=CE,
在△ABF和△DEC中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠ABF=∠DEC}\\{BF=CE}\end{array}\right.$,
∴△ABF≌△DEC(AAS),
∴AF=DC.
点评 本题考查了全等三角形的判定与性质,平行四边形的判定与性质,熟练运用性质与判定方法并确定出平行四边形求解更简便.


科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是( )
如图,?ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是( )| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |α|>2且|β|>2 | B. | |α|+|β|>4$\sqrt{2}$ | C. | |α|>$\frac{5}{2}$或|β|>$\frac{5}{2}$ | D. | |α|>2且|β|<2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com