

分析 (1)取AC的中点D,连接BD,设BC=$\sqrt{3}$x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BD,从而得出结论;
(2)如图2中,首先证明AE是△APQ的中线,设PE=QE=x,则AE=PQ=2x,推出AC=AE+CE=3x,AB=BC=$\frac{3x}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$x,PC=$\sqrt{2}$x,BP=BC-PC=$\frac{\sqrt{2}}{2}$x,由此即可解决问题.
解答 解:(1)如图1中,取AC的中点D,连接BD,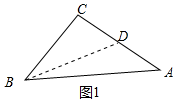
∵∠C=90°,tanA=$\frac{\sqrt{3}}{2}$,
∴$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,
∴设BC=$\sqrt{3}$x,则AC=2x,
∵D是AC的中点,
∴CD=$\frac{1}{2}$AC=x
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{(\sqrt{3}x)^{2}+{x}^{2}}$=2x,
∴AC=BD
∴△ABC是“好玩三角形”;
(2)如图2中,连接AC.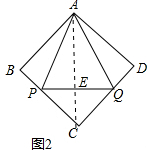
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=90°,
∵PB=DQ,
∴△ABP≌△ADQ,PC=CQ,
∴AP=AQ,
∴AC垂直平分线段PQ,
∴AE是△APQ的中线,易知△PCE,△CEQ,△ACB都是等腰直角三角形,
设PE=QE=x,则AE=PQ=2x,
∴AC=AE+CE=3x,
AB=BC=$\frac{3x}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$x,PC=$\sqrt{2}$x,BP=BC-PC=$\frac{\sqrt{2}}{2}$x,
∴$\frac{BP}{AB}$=$\frac{\frac{\sqrt{2}}{2}x}{\frac{3\sqrt{2}}{2}x}$=$\frac{1}{3}$.
点评 本题四边形综合运用的试题,考查了相似三角形的判定及性质的运用,勾股定理的运用,等腰直角三角形的性质的运用,等腰三角形的性质的运用,锐角三角形函数值的运用,解答时灵活运用三角函数值建立方程求解是解答的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:选择题
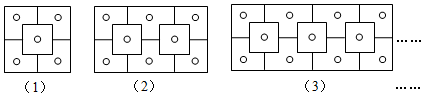
| A. | 32个 | B. | 33个 | C. | 34个 | D. | 35个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届山东省济宁市阶段教育学校统一招生考试数学模拟试卷(解析版) 题型:单选题
将一副三角尺(在RtΔABC中,∠ACB=90°,∠B=60°;在RtΔEDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将RtΔEDF绕点D顺时针方向旋转角α(0°<α<60°), DE?交AC于点M,DF?交BC于点N,则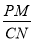 的值为( )
的值为( )
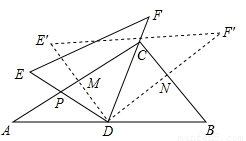
A. 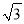 B.
B. 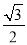 C.
C. 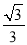 D.
D. 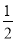
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com