
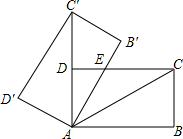
 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若DE=1,则矩形ABCD的面积为3$\sqrt{3}$.
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若DE=1,则矩形ABCD的面积为3$\sqrt{3}$. 分析 根据旋转的性质得到AC=AC′,由AC的中点恰好与D点重合,得到AD=$\frac{1}{2}$AC,根据三角函数的定义得到∠DAE=∠ACD=30°,求得AD=$\sqrt{3}$,AE=2,AE=CE=2,根据矩形的面积公式即可得到结论.
解答 解:∵将矩形ABCD绕点A旋转至矩形AB′C′D′位置,
∴AC=AC′,
∵AC的中点恰好与D点重合,
∴AD=$\frac{1}{2}$AC,
∴∠DAE=∠ACD=30°,
∵DE=1,
∴AD=$\sqrt{3}$,AE=2,
∵∠DAC=90°-30°=60°,
∴∠EAC=30°,
∴∠EAC=∠ACD=30°,
∴AE=CE=2,
∴CD=3,
∴矩形ABCD的面积=CD•AD=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查了旋转的性质、矩形的性质、特殊角的三角函数,三角形面积计算等知识点,难度不大.清楚旋转的“不变”特性是解答的关键.


科目:初中数学 来源: 题型:解答题
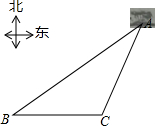 如图,在海中有一个小岛,在它周围6nmile有暗礁,渔船跟踪鱼群由西向东航行,在B处测得小岛A在北偏东55°方向,航行6n mile到达C点,这是测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?(参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80)
如图,在海中有一个小岛,在它周围6nmile有暗礁,渔船跟踪鱼群由西向东航行,在B处测得小岛A在北偏东55°方向,航行6n mile到达C点,这是测得小岛A在北偏东29°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?(参考数据:tan29°≈0.55,tan35°≈0.70,tan55°≈1.43,tan61°≈1.80)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期(10月) | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
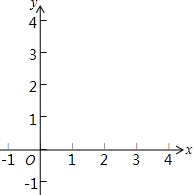 如图,在平面直角坐标系中,已知点A(1,0),B(3,2),请在图中画出线段AB,并在y轴上找一点P,使得PA=PB.(要求:尺规作图,并保留作图痕迹)
如图,在平面直角坐标系中,已知点A(1,0),B(3,2),请在图中画出线段AB,并在y轴上找一点P,使得PA=PB.(要求:尺规作图,并保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+5)(y-5)=x-25 | B. | (x+y)2(x-y)2=x4-2x2y2+y4 | ||
| C. | 6m3÷(-3m2)•(2m)2=4m3 | D. | (8x3-4x2-2x)÷(-2x)=-4x2+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2-1=-2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x-2}$有意义的x的取值范围是x<2 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com