
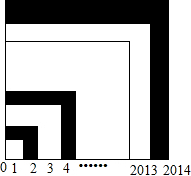
 如图,边长分别为1,2,3…2013,2014的正方形叠放一起,求图中阴影部分的面积.
如图,边长分别为1,2,3…2013,2014的正方形叠放一起,求图中阴影部分的面积. 分析 第一个阴影部分的面积等于第二个图形的面积减去第一个图形的面积,第二个阴影部分的面积等于第四个图形的面积减去第三个图形的面积,由此类推,最后一个阴影部分的面积等于最后一个图形的面积减去倒数第二个图形的面积,由此规律计算得出答案即可.
解答 解:图中阴影部分的面积为:
(22-1)+(42-32)+…+(20142-20132)
=(2+1)(2-1)+(4+3)(4-3)+…+(2014+2013)(2014-2013)
=1+2+3+4+…+2013+2014
=$\frac{1}{2}$×2014×(2014+1)
=2029105.
点评 题考查图形的变化规律,得出每一个阴影部分的面积等于两个正方形面积的差,这样可以将阴影部分的面积看做边长为偶数的正方形的面积减去边长为奇数的正方形的面积解决问题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com