
 过点A(1,2)的直线与双曲线y=$\frac{2}{x}$在第一象限内交于点P,直线AO交双曲线的另一分支于点B,且点C(2,1).
过点A(1,2)的直线与双曲线y=$\frac{2}{x}$在第一象限内交于点P,直线AO交双曲线的另一分支于点B,且点C(2,1).分析 (1)由点A(1,2),点C(2,1),直接利用待定系数法,即可求得直线AC的解析式,继而求得点E的坐标,然后由过点A(1,2)的直线与双曲线y=$\frac{2}{x}$在第一象限内交于点P,求得直线BC的解析式,继而求得答案;
(2)首先设P(m,$\frac{2}{m}$),且m≠1,2,即可求得直线AP与直线BP的解析式,然后进行角关系的转化即可得出结论.
解答 (1)证明:设直线AC的解析式为:y=kx+b,
∵点A(1,2),点C(2,1),
∴$\left\{\begin{array}{l}{k+b=2}\\{2k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为:y=-x+3,
∴点E的坐标为:(0,3);
直线BC的解析式为:y=mx+n,
∵过点A(1,2)的直线与双曲线y=$\frac{2}{x}$在第一象限内交于点P,
∴点B的坐标为:(-1,-2),
∴$\left\{\begin{array}{l}{2k+b=1}\\{-k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴直线BC的解析式为:y=x-1,
∴点F的坐标为:(0,-1);
∴CE=$\sqrt{{2}^{2}+(3-1)^{2}}$=2$\sqrt{2}$,CF=$\sqrt{{2}^{2}+[1-(-1)]^{2}}$=2$\sqrt{2}$,
∴CE=CF;
(2)解:∵P在双曲线上,且不同于A,C两点,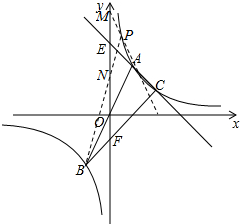
设P(m,$\frac{2}{m}$),且m≠1,2,
∴直线AP可表示为:y=-$\frac{2x}{m}$+$\frac{2}{m}$+2,
直线BP可表示为:y=$\frac{2x}{m}$+$\frac{2}{m}$-2,
①当P点在A点上方时,
连结AP并延长交y轴于M点,连结PB交y轴于N点,
根据直线AP和直线BP的方程可知,M(0,$\frac{2}{m}$+2),N(0,$\frac{2}{m}$-2),
则根据勾股定理可得PM=$\sqrt{(\frac{2}{m}+2-\frac{2}{m})^{2}+{m}^{2}}$=$\sqrt{4+{m}^{2}}$,
同理可得PN=$\sqrt{4+{m}^{2}}$,
∴PM=PN,
∴∠PMN=∠PNM,
∵∠MAE+∠PMN=∠CEF,∠PBC+∠BNF=∠CFE,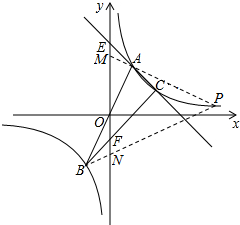
∠MAE=∠PBC,∠CEF=∠CFE,
∴∠PAE=∠PBC,
∵∠PAE+∠PAC=180°,
∴∠PAC+∠PBC=180°.
②当P点在A点下方时,
连结PA并延长交y轴于M点,连结PB交y轴于N点,
同上述方法可得PM=PN,
∴∠PMN=∠PNM,
∵∠MAE+∠CEF=∠PMN,∠PBC+∠BFN=∠PNM,
∠MAE=∠PAC,∠BFN=∠CFE,
∴∠PAC=∠PBC.
点评 此题属于反比例函数综合题.考查了待定系数求函数解析式的知识以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
| 长x(m) | 4 | 3 | 2.5 | 2 | x |
| 另一边长(m) | |||||
| 面积S(m2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该卡标号小于6 | B. | 该卡标号大于6 | C. | 该卡标号是奇数 | D. | 该卡标号是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
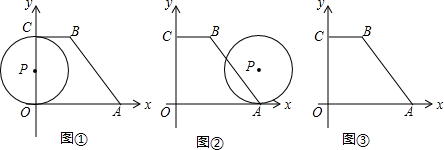
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com