Question

如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重

合，∠OAB＝90°，OA＝4，AB＝2，把Rt△OAB绕点O逆时针旋转90°，点B旋转到

点C的位置，一条抛物线正好经过点O，C，A三点．

（1）求该抛物线的解析式；

（2）在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点M，分

别过点P，点M作x轴的垂线，交x轴于E，F两点，问：四边形PEFM的周长

是否有最大值?如果有，请求出最值，并写出解答过程；如果没有，请说明理由．

（3）如果x轴上有一动点H，在抛物线上是否存在点N，使O（原点）、C、H、N四点

构成以OC为一边的平行四边形，若存在，求出N点的坐标；若不存在，请说明

理由.

Answer 1

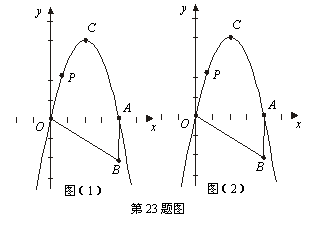
解：（1）因为OA=4，AB=2，把△AOB绕点O逆时针旋转90°，

可以确定点C的坐标为（2，4）；由图可知点A的坐标为

(4，0)，又因为抛物线经过原点，故设y=ax²+bx把(2，4)，

(4，0)代入，得，解得

所以抛物线的解析式为y=-x²+4x

（2）由题意，如图所示，设点P的坐标为P（a，-a²+4a）则

由抛物线的对称性知OE=AF，所以EF=PM=4-2a，

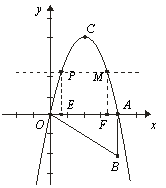PE=MF=-a²+4a，则矩形PEFM的

周长L=2[4-2a+(-a²+4a)]=-2(a-1)²+10

所以当a=1时，矩形PEFM的周长

有最大值，L_max=10

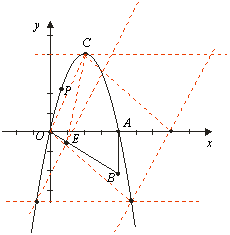
（3）∵y=-x²+4x=-(x-2)²+4

可知顶点坐标（2，4），所以

知道C点正好是顶点坐标，

知道C点到x轴的距离为4个

单位长度，过点C作x轴的平

行线，与x轴没有其它交点，过y=-4作x轴的平行线，与抛

物线有两个交点，这两个交点为所求的N点坐标所以有

-x²+4x=-4 解得x₁=2+，x₂=2-

∴N点坐标为

N₁(2+，-4)，

N₂(2-，-4)