
����Ŀ��ij��վ����A��B�������������շѷ�ʽ��
�շѷ�ʽ | ��ʹ�÷�/Ԫ | ��ʱ����ʱ��/h | ��ʱ��/��Ԫ/min�� |
A | 30 | 25 | 0.05 |
B | m | n | P |
��ÿ������ѧϰʱ��Ϊx��h��Сʱ������A��B���շѽ��ֱ�ΪyA ��Ԫ����yB��Ԫ����
��ͼ��yB��x֮�亯����ϵ��ͼ��
��������ʾ�����ۼ�����ʱ�䲻��������ʱ����ʱ�䡱����ֻ�ա���ʹ�÷ѡ������ۼ�����ʱ�䲻��������ʱ����ʱ�䡱����Գ��������ټ��ա���ʱ�ѡ���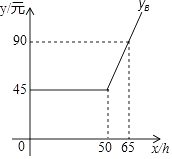
��1��m=��n=p= ��
��2��д��yA��x֮��ĺ�����ϵʽ��
��3����ÿ��������ʱ��Ϊ29Сʱ����˵��ѡȡ���ַ�ʽ�ܽ�ʡ�����ѣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�Խ���BD�Ͻ�ȡBE=BC������CE���ӳ���AD�ڵ�F������AE����B��BG��AE�ڵ�G����AD�ڵ�H�������н��۴�����ǣ�������
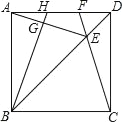
A. AH=DF B. S�ı���EFHG=S��DCF+S��AGH
C. ��AEF=45�� D. ��ABH�ա�DCF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
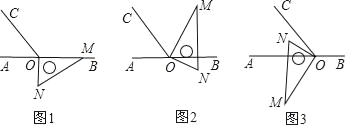
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=112������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC���ʣ�����ON�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��4�����ٶ�����ʱ�뷽����ת��ͼ3��ʹ����ONǡ��ƽ����ǡ�AOC�����ʱ��תһ�����˶���ʱ�䣿
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ�����̽������AOM���NOC֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ1��ͼ2�ṩ��ij��˾��һЩ��Ϣ������������⣮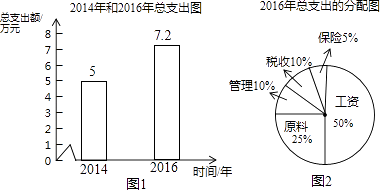
��1��2016��ù�˾����֧���Ľ������Ԫ��
��2��2014�굽2016��ù�˾��֧������ƽ�������ʣ�
��3�����������������ٶȣ�����Ԥ���ù�˾2017�����֧����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��ǽ��AOB��OA��OB����OA��OB���Ȳ��ޣ��У�Ҫ��20m����ǽ����ֱ��ǽ��AOBΧ�ɵ���Ϊ���εĴ��֣��ҵ������AOBC�����Ϊ96m2 �� 
��1�����������εij���
��2���й��Ϊ0.80��0.80��1.00��1.00����λ��m���ĵذ�ש���۷ֱ�Ϊ55Ԫ/���80Ԫ/�飬��ֻѡ����һ�ֵذ�ש��ǡ�����������ֵľ��ε��棨���Ʒ�϶��������һ�ֹ��ĵذ�ש���ý��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABC�У�D��BC���е㣬DE��BC������ΪD����AB�ڵ�E����BE2��EA2��AC2��
(1)��֤����A��90��.
(2)��DE��3��BD��4����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̲ĵھ�����̽���˷���ʽʱ��������ͼ������IJ�ͬ��ʾ������֤�˳˷���ʽ���ҹ���������ѧ����ˬ�����ڹ�Ԫ3���ͣ��Ͱ�һ�����ηֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ĸ�ȫ�ȵ�ֱ��������ƴ����һ�����������(��ͼ��)�����ͼ�γ�Ϊ��ˬ��ͼ����֤��һ���dz���Ҫ�Ľ��ۣ���ֱ������������ֱ�DZ�a��b��б��c�����ϵʽa2��b2��c2����Ϊ���ɶ�����
(1)�����Խ��С�������ĸ�ȫ�ȵ�ֱ��������ƴ������һ�����������(��ͼ��)��Ҳ����֤������ۣ��������С�������֤�Ĺ��̣�
(2)С���ְ����ĸ�ȫ�ȵ�ֱ��������ƴ����һ������(��ͼ��)����������̽�����ý��ۣ���a��3��b��4ʱ����ABCD���ܳ���
(3)��ͼ�ܣ���ÿ��С�����α߳�Ϊ1�ķ���ֽ�У���ABC�Ķ��㶼�ڷ���ֽ����ϣ�����ͼ�л�����ABC�ĸ�BD����������Ľ��ۣ����BD�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c�IJ���ͼ����ͼ��ʾ�������x�ķ���ax2+bx+c=0���������ĺ�Ϊ �� 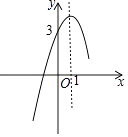
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b�뷴��������y= ![]() ��m��0����ͼ���ڵ�A��3��1�����ҹ���B��0����2����
��m��0����ͼ���ڵ�A��3��1�����ҹ���B��0����2����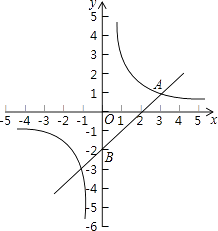
��1������������һ�κ����ı���ʽ��
��2�������P��x����һ�㣬�ҡ�ABP�������3�����P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com