某校教学楼共五层,设有左、右两个楼梯口,通常在放学时,若持续不正常,会导致等待通过的人较多,发生拥堵,从而出现不安全因素.通过观察发现位于教学楼二、三楼的七年级学生从放学时刻起,经过单个楼梯口等待人数按每分钟12人递增,6分钟后经过单个楼梯口等待人数按每分钟8人递减;位于四、五楼的八年级学生从放学时刻起,经过单个楼梯口等待人数按每分钟8人递增,6分钟后经过单个楼梯口等待人数按每分钟16人递减.若在单个楼梯口等待人数超过80人,就可能出现安全问题.
(1)若设在楼梯口等待的人数为y(人),时间为t(分),试分别写出七、八年级学生y和t之间的函数关系式,并指出t的取值范围.
(2)若七、八年级学生同时放学,试计算等待人数超过80人所持续的时间.
(3)要使单个楼梯口等待人数不超过80人,则八年级学生最好比七年级迟几分钟放学?
分析:(1)前六分钟时,七年级单个楼梯口等待人数=12×时间;6分钟后七年级单个楼梯口等待人数=6×12-8×超过6分钟的时间,注意应根据等待的人数为非负数得到自变量的取值;
前六分钟时,八年级单个楼梯口等待人数=8×时间;6分钟后七年级单个楼梯口等待人数=6×8-16×超过6分钟的时间,注意应根据等待的人数为非负数得到自变量的取值;
(2)根据同时放学4、5楼不变,但2、3楼需要加八年级的人数,从而得出关系式求出即可;
(3)让(1)(2)得到的式子为80列式求值即可.
解答:解:(1)七年级:y=12t (0≤t≤6),
y=72-8(t-6)=-8t+120 (15≥t>6),
八年级:y=8t (0≤t≤6),
y=48-16(t-6)=144-16t(9≥t>6);
(2)同时放学:七、八年级单个楼梯口等待人数为:y=(12+8)t=20t(t≤6),
y=120-24(t-6)=-24t+264 (9≥t>6),
∵等待人数超过80人时,即y>80,
∴20t>80,
∴t>4,
∴6-4=2分钟,
∴-24t+264>80,
∴t<
,
∵t>6,
∴
-6=
分钟,
∴等待人数超过80人所持续的时间为:2+
=
分钟;
(3)若八年级学生最好比七年级推迟五分钟放学时,即当t=5,
y=12t=12×5=60,第6分钟时,位于教学楼二、三楼的单个楼梯口等待人数为72<80人,6分钟后逐渐减少,
∴八年级学生最好比七年级迟5分钟放学.
点评:此题主要考查了一次函数的应用,正确得出七、八年级在单个楼梯口等待人数与时间的关系式是解题关键.



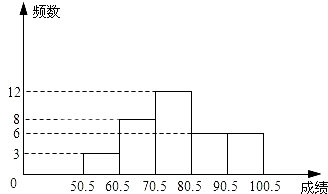 分成五组,并绘制成频数分布直方图(如图所示).
分成五组,并绘制成频数分布直方图(如图所示). 分成五组,并绘制成频数分布直方图(如图所示).
分成五组,并绘制成频数分布直方图(如图所示).