
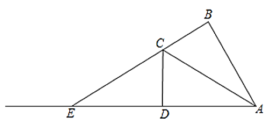
【题目】如图,在四边形ABCD中,AC是对角线,∠ABC=∠CDA=90°,BC=CD,延长BC交AD的延长线于点E.
(1)求证:AB=AD;
(2)若AE=BE+DE,求∠BAC的值;
(3)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P,连接PB.设PB=a,点O是直线AE上的动点,当MO+PO的值最小时,点O与点E是否可能重合?若可能,请说明理由并求此时MO+PO的值(用含a的式子表示);若不可能,请说明理由.
【答案】(1)见解析;(2)22.5°;(3)当MO+PO的值最小时,点O与点E可以重合,见解析,4a
【解析】
(1)证明Rt△ABC≌Rt△ADC即可;
(2)通过等量代换得出△ABE是等腰直角三角形,再由边角关系得出∠BAC的度数即可;
(3)根据题意画出图形,由现有条件得出MC平分∠PME,再根据角平分线的性质得出PC=EC,根据轴对称知识得出点M、点E、点P关于直线AE的对称点Q,这三点共线,也即MO+PO的值最小时,点O与点E重合,最后通过边角运算得出最小值即可.
(1)证明:∵∠ABC=∠CDA=90°,
∵BC=CD,AC=AC,
∴Rt△ABC≌Rt△ADC(HL).
∴AB=AD.
(2)解:∵AE=BE+DE,
又∵AE=AD+DE,
∴AD=BE.
∵AB=AD,
∴AB=BE.
∴∠BAD=∠BEA.
∵∠ABC=90°,
∴∠BAD═45°.
∵由(1)得△ABC≌△ADC,
∴∠BAC=∠DAC.
∴∠BAC═22.5°.
(3)解:当MO+PO的值最小时,点O与点E可以重合,理由如下:
∵ME∥AB,
∴∠ABC=∠MEC=90°,∠MAB=∠EMA.
∵MP⊥DC,
∴∠MPC=90°.
∴∠MPC=∠ADC=90°.
∴PM∥AD.
∴∠EAM=∠PMA.
由(1)得,Rt△ABC≌Rt△ADC,
∴∠EAC=∠MAB,
∴∠EMA=∠AMP.即MC平分∠PME.
又∵MP⊥CP,ME⊥CE,
∴PC=EC.
如图,连接PB,连接PE,延长ME交PD的延长线于点Q.
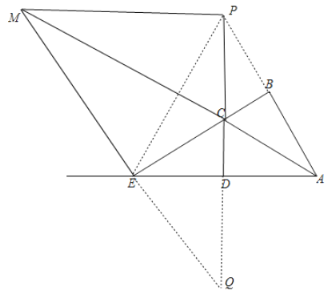
设∠EAM=α,则∠MAP=α.
在Rt△ABE中,∠BEA=90°﹣2α.
在Rt△CDE中,∠ECD=90°﹣∠BEA=2α.
∵PC=EC,
∴∠PEB=∠EPC=∠ECD=α.
∴∠PED=∠BEA+∠PEB=90°﹣α.
∵ME∥AB,
∴∠QED=∠BAD=2α.
当∠PED=∠QED时,
∵∠PDE=∠QDE,DE=DE,
∴△PDE≌△QDE(ASA).
∴PD=DQ.
即点P与点Q关于直线AE成轴对称,也即点M、点E、点P关于直线AE的对称点Q,这三点共线,也即MO+PO的值最小时,点O与点E重合.
因为当∠PED=∠QED时,90°﹣α=2α,也即α=30°.
所以,当∠ABD=60°时,MO+PO取最小值时的点O与点E重合.
此时MO+PO的最小值即为ME+PE.
∵PC=EC,∠PCB=∠ECD,CB=CD,
∴△PCB≌△ECD(SAS).
∴∠CBP=∠CDE=90°.
∴∠CBP+∠ABC=180°.
∴A,B,P三点共线.
当∠ABD=60°时,在△PEA中,
∠PAE=∠PEA=60°.
∴∠EPA=60°.
∴△PEA为等边三角形.
∵EB⊥AP,
∴AP=2AB=2a.
∴EP=AE=2a.
∵∠EMA=∠EAM=30°,
∴EM=AE=2a.
∴MO+PO的最小值为4a.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
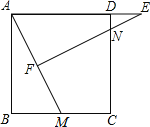
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这两中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅童威准备在一块长为60,宽为48的长方形花圃内修建四条宽度相等,且与各边垂直的小路.四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的8倍.若四条小路所占面积为160.设小路的宽度为x,依题意列方程,化为一般形式为_________
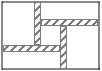
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
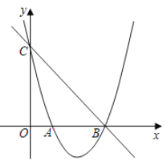
(1)求此抛物线的解析式;
(2)若点![]() 是直线
是直线![]() 下方的抛物线上一动点(不点
下方的抛物线上一动点(不点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
②连接![]() ,
,![]() ,求
,求![]() 的面积最大时点
的面积最大时点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 是抛物线的对称轴上一点,
是抛物线的对称轴上一点,![]() 为
为![]() 轴上一点,是否存在这样的点
轴上一点,是否存在这样的点![]() 和点
和点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?如果存在,请直接写出点
为顶点的四边形是菱形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司拟用运营指数y来量化考核司机的工作业绩,运营指数(y)与运输次数(n)和平均速度(x)之间满足关系式为y=ax2+bnx+100,当n=1,x=30时,y=190;当n=2,x=40时,y=420
用含x和n的式子表示y;
当运输次数定为3次,求获得最大运营指数时的平均速度;
若n=2,x=40,能否在n增加m%(m>0),同时x减少m%的情况下,而y的值保持不变,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
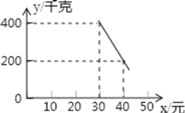
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com