
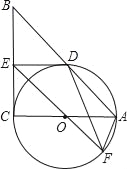
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
【答案】(1)见解析;(2)△ADF的面积是![]() .
.
【解析】试题分析:(1)连接OD,CD,求出∠BDC=90°,根据OE∥AB和OA=OC求出BE=CE,推出DE=CE,根据SSS证△ECO≌△EDO,推出∠EDO=∠ACB=90°即可;
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,求出OM=FN,求出BC、AC、AB的值,根据sin∠BAC=![]() ,求出OM,根据cos∠BAC=
,求出OM,根据cos∠BAC=![]() ,求出AM,根据垂径定理求出AD,代入三角形的面积公式求出即可.
,求出AM,根据垂径定理求出AD,代入三角形的面积公式求出即可.
试题解析:
(1)证明:连接OD,CD,

∵AC是⊙O的直径,
∴∠CDA=90°=∠BDC,
∵OE∥AB,CO=AO,
∴BE=CE,
∴DE=CE,
∵在△ECO和△EDO中
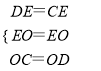 ,
,
∴△ECO≌△EDO,
∴∠EDO=∠ACB=90°,
即OD⊥DE,OD过圆心O,
∴ED为⊙O的切线.
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,
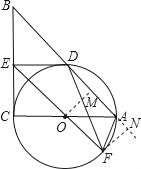
则OM∥FN,∠OMN=90°,
∵OE∥AB,
∴四边形OMFN是矩形,
∴FN=OM,
∵DE=4,OC=3,由勾股定理得:OE=5,
∴AC=2OC=6,
∵OE∥AB,
∴△OEC∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AB=10,
在Rt△BCA中,由勾股定理得:BC=![]() =8,
=8,
sin∠BAC=![]() ,
,
即![]() ,
,
OM=![]() =FN,
=FN,
∵cos∠BAC=![]() ,
,
∴AM=![]()
由垂径定理得:AD=2AM=![]() ,
,
即△ADF的面积是![]() AD×FN=
AD×FN=![]() ×
×![]() ×
×![]() =
=![]() .
.
答:△ADF的面积是![]() .
.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当∠BAC= 时,矩形AEBD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,动点P每次沿着与x轴成45°的方向运动,第一次从原点O向右上方运动1个单位长度到P1(![]() ,
,![]() ),第二次从点P1向右下方运动1个单位长度到P2(
),第二次从点P1向右下方运动1个单位长度到P2(![]() ,0),第三次从点p2向右下方运动2个单位长度到P3(2
,0),第三次从点p2向右下方运动2个单位长度到P3(2![]() ,-
,-![]() ),第四次从点P3向右上方动2个单位长度到P4(3
),第四次从点P3向右上方动2个单位长度到P4(3![]() ,0),第五次从点P4向右上方运动3个单位长度到P5(
,0),第五次从点P4向右上方运动3个单位长度到P5(![]() ,
,![]() ),第六次从点P5向右下方运动3个单位长度到P6(6
),第六次从点P5向右下方运动3个单位长度到P6(6![]() ,0)……依此规律下去,则P43的坐标为( )
,0)……依此规律下去,则P43的坐标为( )

A. (242![]() ,-11
,-11![]() )B. (242
)B. (242![]() ,11
,11![]() )
)
C. (![]() )D. (
)D. (![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大课间是学校的校体课程之一,涉及的范围广,内容繁多。某校根据实际情况决定开设![]() :乒乓球,
:乒乓球,![]() :篮球,
:篮球,![]() :跑步,
:跑步,![]() :跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:
:跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:

(1)补全条形统计图;
(2)制作扇形统计图;
(3)若该校有学生2400人,请问:喜欢打乒乓球的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
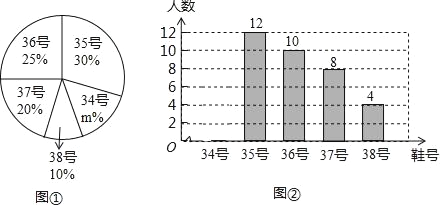
【题目】为了方便学生参加体育锻炼,某学校准备购买一批运动鞋供学生体育锻炼借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下不完整的统计图①和图②,请根据有关信息,解答下列问题:
(1)填空:本次随机抽样调查的学生为 名,本次调查获取的样本数据的中位数是 号,众数是 号;
(2)补全条形统计图;
(3)根据样本数据,若学校计划购买800双运动鞋,建议购买34号运动鞋多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
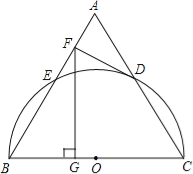
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com