练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且∠D=2∠CAD．

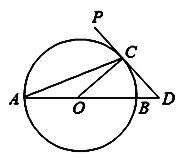
    （1）求∠D的度数；

    （2）若CD=2，求BD的长．

    【答案】（1）45°；（2）．

    【解析】

    试题（1）根据等腰三角形性质和三角形外角性质求出∠COD=2∠A，求出∠D=∠COD，根据切线性质求出∠OCD=90°，即可求出答案；

    （2）求出OC=CD=2，根据勾股定理求出BD即可．

    试题解析：（1）∵OA=OC，

    ∴∠A=∠ACO，

    ∴∠COD=∠A+∠ACO=2∠A，

    ∵∠D=2∠A，

    ∴∠D=∠COD，

    ∵PD切⊙O于C，

    ∴∠OCD=90°，

    ∴∠D=∠COD=45°；

    （2）∵∠D=∠COD，CD=2，

    ∴OC=OB=CD=2，

    在Rt△OCD中，由勾股定理得：22+22=（2+BD）2，

    解得：BD=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们在探究一元二次方程根与系数的关系中发现：如果关于x的方程x2+px+q＝0的两个根是x1，x2，那么由求根公式可推出x1+x2＝﹣p，x1x2＝q，请根据这一结论，解决下列问题：

    （1）若α，p是方程x2﹣3x+1＝0的两根，则α+β＝　 　，αβ＝　 　；若2，3是方程x2+mx+n＝0的两根，则m＝　 　，n＝　 　；

    （2）已知a，b满足a2﹣5a+3＝0，b2﹣5b+3＝0，求的值；

    （3）已知a，b，c满足a+b+c＝0，abc＝5，求正整数c的最小值，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】国贸商店服装柜在销售中发现：“宝乐牌”童装平均每天可以售出20件，每件盈利40元．为了迎接“六一”儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存．经调查发现：每件童装每降价1元，商场平均每天可多销售2件．

    （1）若每件童装降价5元，则商场盈利多少元？

    （2）若商场每天要想盈利1200元，请你帮助商场算一算，每件童装应降价多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

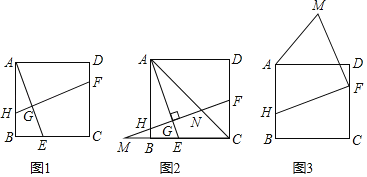
    【题目】在正方形ABCD中，点H，E，F分别在边AB，BC，CD上，AE⊥HF于点G．

    （1）如图1，求证：AE＝HF；

    （2）如图2，延长FH，交CB的延长线于M，连接AC，交HF于N．若MB＝BE，EC＝2BE，求的值；

    （3）如图3，若AB＝2，BH＝DF，将线段HF绕点F顺时针旋转90°至线段MF，连接AM，则线段AM的最小值为　 　．（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在长方形中，＝，＝，点从点开始沿边向终点以的速度移动，与此同时，点从点开始沿边向终点以的速度移动．如果、分别从、同时出发，当点运动到点时，两点停止运动．设运动时间为秒．

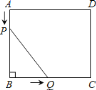
    （1）填空：______＝______，______＝______（用含t的代数式表示）；

    （2）当为何值时，的长度等于？

    （3）是否存在的值，使得五边形的面积等于？若存在，请求出此时的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

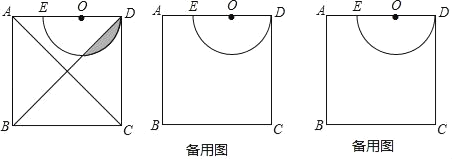
    【题目】如图，已知正方形ABCD的边长是5，点O在AD上，且⊙O的直径是4．

    (1)正方形的对角线BD与半圆O交于点F，求阴影部分的面积；

    (2)利用图判断，半圆O与AC有没有公共点，说明理由．(提示：≈1.41)

    (3)将半圆O以点E为中心，顺时针方向旋转．

    ①旋转过程中，△BOC的最小面积是　　；

    ②当半圆O过点A时，半圆O位于正方形以外部分的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下列材料,然后解答问题．

    材料：从三角形不是等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线．

    例如：如图,AD把分成与,若是等腰三角形,且∽,那么AD就是的完美分割线．

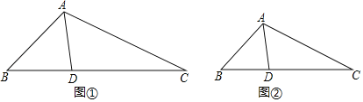
    解答下列问题：

    如图,在中,若∠B=40°,AD是的完美分割线,且是以AD为底边的等腰三角形,则____度；

    在中,若,,AD是的完美分割线,是等腰三角形,则____；

    如图,在中,AD平分,求证AD是的完美分割线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2＋(2k－1)x＋k2＝0有两个实根x1和x2

    (1) 求实数k的取值范围

    (2) 若方程两实根x1、x2满足x12－x22＝0，求k的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______．

    查看答案和解析>>

    同步练习册答案