
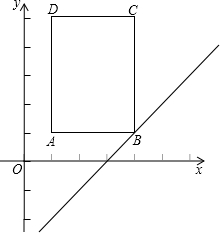
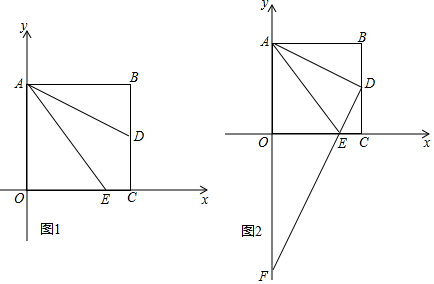
 如图,矩形ABCD在平面直角坐标系中,点A(1,1),B(4,1),C(4,5),D(1,5),将一次函数y=x-3的图象L沿y轴以每秒1个单位的速度向上运动,设运动的时间为t秒,L扫过矩形的面积为S.
如图,矩形ABCD在平面直角坐标系中,点A(1,1),B(4,1),C(4,5),D(1,5),将一次函数y=x-3的图象L沿y轴以每秒1个单位的速度向上运动,设运动的时间为t秒,L扫过矩形的面积为S.分析 (1)先根据平移的方向,设直线y=x-3向上平移t秒后得到的直线为y=x-3+t,再分别把点B和点A的坐标代入计算即可;
(2)分3种情况,利用直角三角形与直角梯形的面积公式进行计算,即可得到S与t之间的函数关系式.
解答 解:(1)设直线y=x-3向上平移t秒后,得到直线y=x-3+t,
把B(4,1)代入y=x-3+t,可得1=4-3+t,
解得t=0,
∴当t=0秒时,L经过点B;
把A(1,1)代入y=x-3+t,可得1=1-3+t,
解得t=3,
∴当t=3秒时,L经过点A;
故答案为:0,3;
(2)同理可得,当t=4秒时,L经过点C;当t=7秒时,L经过点D;
分三种情况:
①当0≤t≤3时,如图,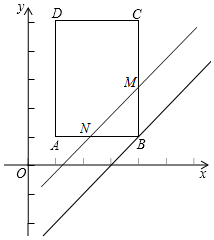
此时MB=t,NB=t,
∴S=${\frac{1}{2}t}^{2}$;
②当3<t≤4时,如图,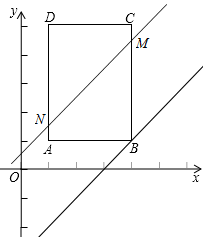
此时,BM=t,AB=3,NA=t-3,
∴S=$\frac{(t-3+t)×3}{2}$=3t-$\frac{9}{2}$;
③当4<t≤7时,DM=3-CM=3-(t-4)=7-t,DN=7-t,
∴S=3×4-$\frac{1}{2}$(7-t)2=-$\frac{1}{2}$t2+7t-$\frac{25}{2}$,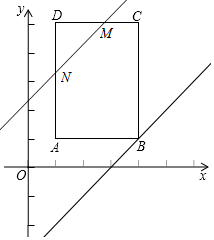
综上所述:S与运动时间t的函数关系为S=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}(0≤t<3)}\\{3t-\frac{9}{2}(3≤t<4)}\\{-\frac{1}{2}{t}^{2}+7t-\frac{25}{2}(4≤t≤7)}\end{array}\right.$.
点评 本题考查了矩形的性质、一次函数图象上点的坐标特征、三角形的面积公式以及直角梯形的面积公式的运用,解题的关键是根据三角形和梯形的面积公式找出S关于t的关系式.解题时注意:需要结合图形的变化按时间t进行分类讨论.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 众数是1.5 | B. | 中位数是3 | C. | 平均数是3 | D. | 方差是$\frac{13}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
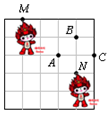 如图,两只福娃发尖所处的位置分别为M(-2,2)、N(1,-1),则A、B、C三个点中为坐标原点的是( )
如图,两只福娃发尖所处的位置分别为M(-2,2)、N(1,-1),则A、B、C三个点中为坐标原点的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{900}{x}$=$\frac{600}{x+30}$ | B. | $\frac{900}{x}$=$\frac{600}{x-30}$ | C. | $\frac{600}{x}$=$\frac{900}{x+30}$ | D. | $\frac{600}{x}$=$\frac{900}{x-30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com