练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    对于用四舍五入法得到的近似数万，下列说法中正确的是（ ）．

    A. 它精确到 B. 它精确到十位 C. 它精确到百位 D. 它精确到万位

    C 【解析】万，所以它精确到了百位， 故选．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：陕西省2018届九年级上学期期中考试数学试卷 题型：填空题

    小华为了测量所住楼房的高度，他请来同学帮忙，在阳光下测量了同一时刻他自己的影长和楼房的影长分别是米和米．已知小华的身高为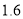米，那么他所住楼房的高度为__________米．

    48 【解析】设楼房的高度为x米，由题意得 1.6:x=0.5:15， 解得x=48， 所以楼房高度是48米.

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型：解答题

    为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：

    收费标准（注：水费按月份结算）

    每月用水量

    单价（元/立方米）

    不超出立方米的部分

    超出立方米不超出立方米的部分

    超出立方米的部分

    例如：某户居民月份用水立方米，应收水费为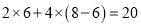（元）．

    请根据上表的内容解答下列问题：

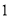    （）若某户居民月份用水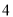立方米，则应收水费多少元？

    （）若某户居民月份用水立方米（其中），请用含的代数式表示应收水费．

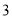    （）若某户居民、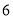两个月共用水立方米（月份用水量超过了立方米），设月份用水立方米，请用含的代数式表示该居民、两个月共交水费多少元．

    （）应收水费为8元；（）元；（）见解析. 【解析】试题分析：（1）用水4立方米，按每立方米2元直接进行计算即可得； （2）分成两部分，前6立方米按照每立方米2元收取；(a-6)立方米按照4元每立方米收取；分别求出各部分需要的费用，再相加即可； （3）应分5月份用水量不超过6m3时，5月份用水超过6m3两种情况进行讨论即可得. 试题解析：（）， ∴应收水费为元； ...

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型：填空题

    比较大小： .

    ＜ 【解析】∵两个负数中绝对值大的反而小， 又∵ =-，=-， ∴ ＞ ， ∴ ＜．

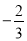    查看答案和解析>>

    科目：初中数学 来源：浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型：单选题

    有长为的篱笆，利用他和房屋的一面墙围成如图形状的长方形园子，园子的宽为，则所围成的园子面积为（ ）．

    A. B. C. D.

    D 【解析】该篱笆围成的园子的长为， ∴园子面积为， 故选．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型：解答题

    如图，在△ABC中，AB＝AC，AC边上的中线BD把△ABC的周长分成12cm和15cm两部分，求△ABC各边的长．

    AB＝AC＝8cm，BC＝11cm或AB＝AC＝10cm，BC＝7cm 【解析】【试题分析】本题目需要分类讨论，设AB＝2xcm，BC＝ycm. (1)当AB＋AD＝12cm，BC＋CD＝15cm， 列方程组得： ,解得，从而得到AB＝AC＝8cm，BC＝11cm. （2）当AB＋AD＝15cm，BC＋CD＝12cm时，列方程组得 解得，AB＝AC＝10cm，BC＝7cm.最后根...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型：填空题

    平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2=________．

    24 【解析】试题分析：正多边形的每个内角都相等，正五边形的每个内角为108°，正六边形的每个内角为120°， 所以∠1=120°-108°=12°；∠2=108°-90°=18°；∠3=90°-60°=30°， 所以∠3＋∠1－∠2＝30°+12°-18°=24°．

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    已知如图，在数轴上点， 所对应的数是， ．

    对于关于的代数式，我们规定：当有理数在数轴上所对应的点为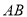之间（包括点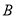， ）的任意一点时，代数式取得所有值的最大值小于等于，最小值大于等于，则称代数式，是线段的封闭代数式．

    例如，对于关于的代数式，当时，代数式取得最大值是；当时，代数式取得最小值是，所以代数式是线段的封闭代数式．

    问题：（）关于代数式，当有理数在数轴上所对应的点为之间（包括点， ）的任意一点时，取得的最大值和最小值分别是__________．

    所以代数式__________（填是或不是）线段的封闭代数式．

    （）以下关的代数式：

    ①；②；③；④．

    是线段的封闭代数式是__________，并证明（只需要证明是线段的封闭代数式的式子，不是的不需证明）．

    （）关于的代数式是线段的封闭代数式，则有理数的最大值是__________，最小值是__________．

    （）见解析（）④（）； 【解析】试题分析：（1）观察数轴，当时， 取得最大值为，当时， 取得最小值为，所以代数式不是线段的封闭代数式； （2）按照封闭代数式的定义，逐个分析即可； （3）观察代数式可知，当时， 取得最大值为，列方程求出x的值；当时， 取得最小值为，列方程求出x的值；然后从中选出最大的和最小的. （）【解析】 当时， 取得最大值为， 当时， 取得...

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州西湖区2016-2017学年七年级上学期期末数学试卷 题型：填空题

    的立方根为__________， 的平方根为__________．

    【解析】试题解析：∵23=8， ∴的立方根为2； ∵（±2）2=4， ∴4的平方根为±2. 故答案为：2，±2.

    查看答案和解析>>

    同步练习册答案