
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A﹙﹣2,﹣5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙﹣2,﹣5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
(3)当kx+b>![]() 时,请写出自变量x的取值范围.
时,请写出自变量x的取值范围.
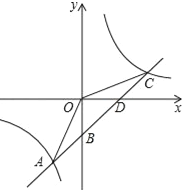
【答案】(1)y=x﹣3;(2)10.5;(3)﹣2<x<0或x>5.
【解析】
(1)由反比例函数y=![]() 的图象经过点A﹙-2,-5﹚可得反比例函数的表达式y=
的图象经过点A﹙-2,-5﹚可得反比例函数的表达式y=![]() ,
,
又点C﹙5,n﹚在反比例函数的图象上可得C的坐标为﹙5,2﹚,而一次函数的图象经过点A、C,将这两个点的坐标代入y=kx+b,可得所求一次函数的表达式为y=x-3;(2)把x=0代入一次函数y=x-3可得B点坐标为﹙0,-3﹚即OB=3又A点的横坐标为-2,C点的横坐标为5,根据S△AOC=S△AOB+S△BOC及三角形的面积公式即可求得△AOC的面积;(3)观察图象,直接可得结论.
(1)把A﹙﹣2,﹣5﹚代入y=![]() 得:m=10,
得:m=10,
即反比例函数的表达式为y=![]() ,
,
把C﹙5,n﹚代入y=![]() 得:n=2,
得:n=2,
即C(5,2),
把A.C的坐标代入y=kx+b得:![]() ,
,
解得:k=1,b=﹣3,
所以一次函数的表达式为y=x﹣3;
(2)把x=0代入y=x﹣3得:y=﹣3,即OB=3,
∵C(5,2),A﹙﹣2,﹣5﹚,
∴△AOC的面积为![]() ×3×|﹣2|+
×3×|﹣2|+![]() ×3×5=10.5;
×3×5=10.5;
(3)由图象可知:当kx+b>![]() 时,自变量x的取值范围是﹣2<x<0或x>5.
时,自变量x的取值范围是﹣2<x<0或x>5.


科目:初中数学 来源: 题型:
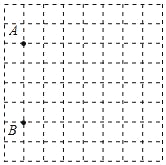
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
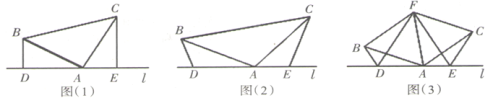
【题目】(1)问题发现:如图(1),已知:在三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() ,试写出线段
,试写出线段![]() 和
和![]() 之间的数量关系为_________________.
之间的数量关系为_________________.
(2)思考探究:如图(2),将图(1)中的条件改为:在![]() 中,
中, ![]() 三点都在直线
三点都在直线![]() 上,并且
上,并且![]() ,其中
,其中![]() 为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展应用:如图(3),![]() 是
是![]() 三点所在直线
三点所在直线![]() 上的两动点,(
上的两动点,(![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 与
与![]() 均为等边三角形,连接
均为等边三角形,连接![]() ,若
,若![]() ,试判断
,试判断![]() 的形状并说明理由.
的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACE是以平行四边行ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(10,-4![]() ),则D点的坐标是( )
),则D点的坐标是( )

A.(6,0)B.(6![]() ,0)C.(8,0)D.(8
,0)C.(8,0)D.(8![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
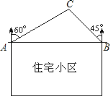
【题目】某住宅小区如图所示,小区东西两端的楼![]() 、
、![]() 之间的距离为
之间的距离为![]() ,某开发商准备在位于
,某开发商准备在位于![]() 楼的北偏东
楼的北偏东![]() 方向,且在
方向,且在![]() 楼的北偏西
楼的北偏西![]() 方向上的
方向上的![]() 处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆
处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆![]() 处.请你通过计算说明住宅小区是否会有住户受到噪音的影响.(参考数据
处.请你通过计算说明住宅小区是否会有住户受到噪音的影响.(参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
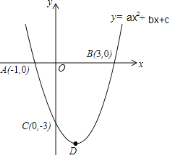
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,![]() 为抛物线的顶点.
为抛物线的顶点.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 抛物线的对称轴上是否存在一点
抛物线的对称轴上是否存在一点![]() ,使
,使![]() 为等腰三角形?若存在,写出点
为等腰三角形?若存在,写出点![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
![]() 点
点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() ,求四边形
,求四边形![]() 面积的最大值,以及此时点
面积的最大值,以及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com