(1)计算:-1-$\root{3}{27}$-0+$\sqrt{3}$tan30°(2)解方程:$\frac{x-3}{x-2}$+1=$\frac{3}{x-2}$．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

11．（1）计算：（$\frac{1}{2}$）^-1-$\root{3}{27}$-（π-2017）⁰+$\sqrt{3}$tan30°
（2）解方程：$\frac{x-3}{x-2}$+1=$\frac{3}{x-2}$．

分析（1）原式利用零指数幂、负整数指数幂法则，立方根定义，以及特殊角的三角函数值计算即可得到结果；
（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答解：（1）原式=2-3-1+1=-1；

（2）去分母得：x-3+x-2=3，
解得：x=4，
经检验x=4是分式方程的解．

点评此题考查了解分式方程，以及实数的运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

1．计算：$[（-\frac{1}{3}）^{501}]^{4}×{3}^{2003}$=$\frac{1}{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．

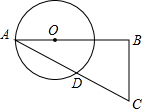如图所示，BD是⊙O的切线，AE是⊙O的直径，AD是一条非直径的弦，过点B作BC⊥AB，BC与AD的延长线相交于点C，
（1）若BE=$\frac{1}{2}$AE，求∠EAD的度数；
（2）求证：AC•AD=AB•AE；
（3）在（1）条件下，当BC=2时，求四边形BCDE的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

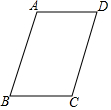如图，四边形ABCD是平行四边形．
（1）请用直尺和圆规按下列步骤作图，保留作图痕迹：
①作∠BAD的平分线，交CD于E，交BC的延长线于F；②连接BE；
（2）在（1）作出图形中，若∠F=45°，AB=8，DE=5，求四边形ABCD的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．先化简，再求值：$\frac{{x}^{2}-6x+9}{{x}^{2}-9}$÷$\frac{x-3}{2}$，其中x=-2．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．计算：（2$\sqrt{2}$）²+2cos45?-（$\frac{1}{2}$）^-1-|1-$\sqrt{2}$|-（π-3.14）⁰．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

3．

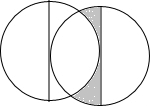半径为1的两圆放置位置如图所示，一圆的直径恰好是另一圆的切线，圆心均为切点，则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．

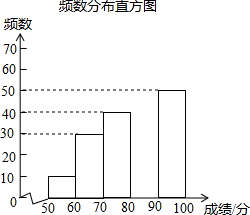为了传承优秀传统文化，我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩x/分	频数	频率
50≤x＜60	10	0.05
60≤x＜70	30	0.15
70≤x＜80	40	n
80≤x＜90	m	0.35
90≤x≤100	50	0.25

请根据所给信息，解答下列问题：
（1）m=70，n=0.2；
（2）请补全频数分布直方图；
（3）这次比赛成绩的中位数会落在80≤x＜90分数段；
（4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

1．某同学在用描点法画二次函数y=ax²+bx+c的图象时，列出下面的表格：

x	…	-5	-4	-3	-2	-1	…
y	…	-7.5	-2.5	0.5	1.5	0.5	…

根据表格提供的信息，有下列结论：
①该抛物线的对称轴是直线x=-2；②该抛物线与y轴的交点坐标为（0，-2.5）；③b²-4ac=0；④若点A（0.5，y₁）是该抛物线上一点．则y₁＜-2.5．则所有正确的结论的序号是①②④．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学