
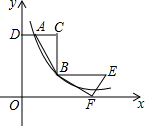
 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,延长CA交y轴于点D,AD=1.分析 (1)设A(1,k),再表示出B(3,k-4),则利用反比例函数图象上点的坐标特征得到3(k-4)=k,解方程求出k即可得到该反比例函数的解析式;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,根据旋转的性质得BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,再计算出BM=CM-BC=2,则在Rt△BMF中,利用三角函数可求出∠MBF=60°,MF=$\sqrt{3}$BM=2$\sqrt{3}$,于是得到旋转角为120°,然后证明Rt△BMF∽Rt△FNE,利用相似比求出FN和EN,从而可得到E点坐标.
解答 解:(1)∵AC∥x轴,AD=1,
∴A(1,k),
∵∠C=90°,AC=2,BC=4,
∴B(3,k-4),
∵点B在y=$\frac{k}{x}$的图象上,
∴3(k-4)=k,解得k=6,
∴该反比例函数的解析式为y=$\frac{6}{x}$;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,
∵△ABC绕点B顺时针旋转得到△EBF,
∴BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,
∵BC⊥x轴,A(1,6),
∴BM=CM-BC=6-4=2,
在Rt△BMF中,∵cos∠MBF=$\frac{MB}{BF}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠MBF=60°,MF=$\sqrt{3}$BM=2$\sqrt{3}$,
∴∠CBF=180°-∠MBF=120°,
∴旋转角为120°;
∵∠BFM+∠MBF=90°,∠BFM+∠EFN=90°,
∴∠MBF=∠EFN,
∴Rt△BMF∽Rt△FNE,
∴$\frac{BM}{FN}$=$\frac{MF}{EN}$=$\frac{BF}{EF}$,即$\frac{2}{FN}$=$\frac{2\sqrt{3}}{NE}$=$\frac{4}{2}$,
∴FN=1,EN=$\sqrt{3}$,
∴ON=OM+MF+FN=3+2$\sqrt{3}$+1=4+2$\sqrt{3}$,
∴E点坐标为(4+2$\sqrt{3}$,$\sqrt{3}$).
点评 本题考查了用待定系数法求反比例函数的解析式:先设出含有待定系数的反比例函数解析式y=xk(k为常数,k≠0);再把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;接着解方程,求出待定系数;然后写出解析式.也考查了旋转的性质.解决本题的关键是作BM⊥x轴于M,EN⊥x轴于N,构建Rt△BMF∽Rt△FNE.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
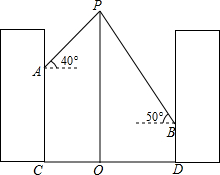 如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
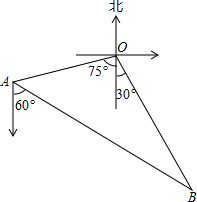 如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?
如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
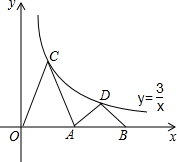 如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.
如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
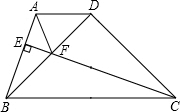 如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.
如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com