
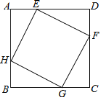
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别在正方形的四条边上,且
分别在正方形的四条边上,且![]() ,则四边形
,则四边形![]() 的形状为________,它的面积的最小值为________.
的形状为________,它的面积的最小值为________.
【答案】正方形![]()
【解析】
先证明△AEH≌△DFE≌△CGF≌△BHG,从而得到HE=EF=FG=HG,然后证明EFGH四边形有一个角是直角,从而可判断出四边形EFGH的形状,设AE=x,则AH=(![]() -x),依据正方形的面积公式以及勾股定理可得到四边形EFGH的面积与x的函数关系式,依据二次函数的性质求得二次函数的最小值即可.
-x),依据正方形的面积公式以及勾股定理可得到四边形EFGH的面积与x的函数关系式,依据二次函数的性质求得二次函数的最小值即可.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD, ∠A=∠B=∠C=∠D.
∵AE=DF=CG=BH,
∴AH=ED=FG=BG.
在△AEH、△DFE、△CGF、△BHG中, ,
,
∴△AEH≌△DFE≌CGF≌△BHG.
∴HE=EF=FG=HG.
∴四边形EFGH是菱形.
∵△AEH≌△DFE,
∴∠AEH=∠DFE.
∵∠AHE+∠AEH=90°,
∴∠DEF+∠AEH=90°.
∴∠HEF=90°.
∴EHGF为正方形.
设AE=x,则AH=(![]() -x).
-x).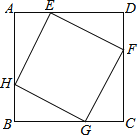
∵正方形EFHG的面积=HE=AE+AH=x+(![]() -x) =2x-2
-x) =2x-2![]() x+5,
x+5,
∴当x=![]() 时,正方形的面积有最小值.
时,正方形的面积有最小值.
∴正方形EFHG的面积的最小值=![]() .
.
故答案为:正方形;![]() .
.


科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示根据图象信息给出下列说法:

①每分钟进水5升;
②当![]() 时,容器中水量在减少;
时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以下说法中正确的有( )
A.①B.①②C.①④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平
方式的和,这种方法称之为配方法,例如:可将多项式![]() 通过横档变形化为
通过横档变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
(1)(理解)对于多项式![]() ,当x=____________时,它的最小值为______________.
,当x=____________时,它的最小值为______________.
(2)(应用)若![]() ,求
,求![]() 的值.
的值.
(3)(拓展)![]() 是
是![]() 的三边,且有
的三边,且有![]() .
.
①若c为整数,求c的值.
②直接写出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年“国际攀岩比赛”在重庆举行.小丽从家出发开车前去观看,途中发现忘了带门票,于是打电话让妈妈马上从家里送来,同时小丽也往回开,遇到妈妈后聊了一会儿,接着继续开车前往比赛现场.设小丽从家出发后所用时间为t,小丽与比赛现场的距离为S.下面能反映S与t的函数关系的大致图象是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:
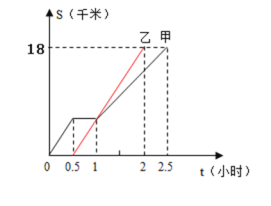
(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-![]() 平行.
平行.
(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-![]() 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com