
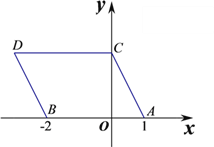
【题目】如图,在平面直角坐标系中,点![]() 的坐标分别为(1,0)、(-2,0),现同时将点
的坐标分别为(1,0)、(-2,0),现同时将点![]() 分别向上平移2个单位,再向左平移1个单位,分别得到点
分别向上平移2个单位,再向左平移1个单位,分别得到点![]() 的对应点
的对应点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)若在![]() 轴上存在点
轴上存在点![]() ,连接
,连接![]() ,使S△ABM =S□ABDC,求出点
,使S△ABM =S□ABDC,求出点![]() 的坐标;
的坐标;
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,求S=S△PCD+S△POB的取值范围;
,求S=S△PCD+S△POB的取值范围;
(3)若![]() 在直线
在直线![]() 上运动,请直接写出
上运动,请直接写出![]() 的数量关系.
的数量关系.
【答案】(1)(0,4)或(0,-4);(2)![]() ;(3)答案见解析
;(3)答案见解析
【解析】(1)先根据S△ABM =S□ABDC,得出△ABM的高为4,再根据三角形面积公式得到M点的坐标;
(2)先计算出S梯形OBDC=5,再讨论:当点P运动到点B时,S△POC的最小值=2,当点P运动到点D时,S△POC的最大值=3,即可判断S=S△PCD+S△POB的取值范围的取值范围;
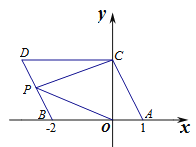
(3)分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO-∠EPC=∠BOP-∠DCP,于是∠BOP-∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP-∠BOP=∠CPO.
解:(1)由题意,得C(0,2)
∴□ABDC的高为2
若S△ABM =S□ABDC,则△ABM的高为4
又∵点M是y轴上一点
∴点M的坐标为(0,4)或(0,-4)
(2)∵B(-2,0),O(0,0)
∴OB=2
由题意,得C(0,2),D(-3,2)
∴OC=2,CD=3
∴S梯形OBDC=![]()
点![]() 在线段
在线段![]() 上运动,
上运动,
当点![]() 运动到端点B时,△PCO的面积最小,为
运动到端点B时,△PCO的面积最小,为![]()
当点![]() 运动到端点D时,△PCO的面积最大,为
运动到端点D时,△PCO的面积最大,为![]()
∴S=S△PCD+S△POB= S梯形OBDC-S△PCO=5-S△PCO
∴S的最大值为5-2=3,最小值为5-3=2
故S的取值范围是:![]()
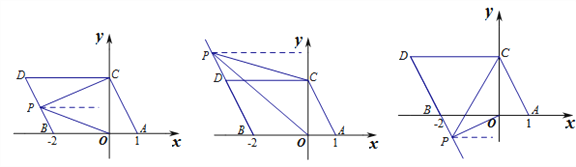
(3)如图:
当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]()
当点![]() 在射线
在射线![]() 上运动时,
上运动时,![]()
当点![]() 在射线
在射线![]() 上运动时,
上运动时,![]()


科目:初中数学 来源: 题型:
【题目】小华准备购买单价分别为4元和5元的两种拼装饮料,若小华将50元恰好用完,两种饮料都买,则购买方案共有( )
A. 2种 B. 3种 C. 4种 D. 5种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)
(1) 填空:
(a-b)(a+b)=________;
(a-b)(a2+ab+b2)=________;
(a-b)(a3+a2b+ab2+b3)=________.
(2) 猜想:
(a-b)(an-1+an-2b+…+abn-2+bn-1)=________ (其中n为正整数,且n≥2).
(3) 利用(2)猜想的结论计算: 29-28+27-…+23-22+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在半径为R的圆形钢板上,挖去四个半径都为r的小圆.若R=16.8,剩余部分的面积为272π,则r的值是( )
A. 3.2 B. 2.4 C. 1.6 D. 0.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年初,某服装经销商发现某款新型运动服市场需求量较大,该服装的进价为200元/件,每年支付员工工资和场地租金等其它费用总计40000元.经过市场调查发现若销售单价为x元/件,则年销售量为(800-x)件.
(1)用含x的代数式表示年获利金额w;
(注:年获利=(销售单价-进价)×年销售量-其它费用)
(2)若经销商希望该服装一年的销售获利达40000元,且要使产品销售量较大,你认为销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩子政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度,在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
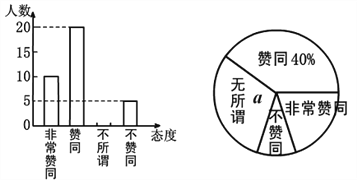
(1)在这次问卷调查中一共抽取了__________名学生,a=________%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com