
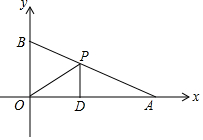
 如图,直线y=-$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,点D在x轴上,P是线段AB上的动点,连接DP,OP,过点O作OE平行PD,过点D作DE平行OP得平行四边形OPDE.
如图,直线y=-$\frac{1}{2}$x+2与x轴,y轴分别交于A,B两点,点D在x轴上,P是线段AB上的动点,连接DP,OP,过点O作OE平行PD,过点D作DE平行OP得平行四边形OPDE.分析 (1)如图1中,连接PE交OD于H.根据菱形的性质可知H(1,0),由此即可求出P的坐标.
(2)①如图2中,连接PE交OD于H.由四边形OPDE是正方形,不妨设PH=OH=DH=x,由PH∥OB,推出$\frac{PH}{OB}$=$\frac{AH}{AO}$,可得$\frac{x}{2}$=$\frac{4-x}{4}$,解方程即可解决问题.
②如图3中,如图以OD为直径作⊙H,当⊙H与AB相切时,存在唯一位置使得平行四边形OPDE是矩形.由AB是⊙H的切线,OB是⊙H的切线,推出BO=BP=2.在Rt△AOB中,AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,推出AP=$\sqrt{5}$-2,设OH=PH=x,在Rt△APH中,根据AP2+PH2=AH2,可得方程($\sqrt{5}$-2)2+x2=(4-x)2,解方程即可解决问题.
解答 解:(1)如图1中,连接PE交OD于H.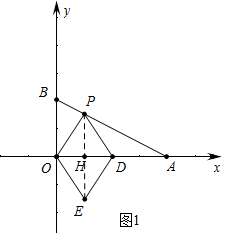
∵D(2,0),
∴OD=2,
∵四边形OPDE是菱形,
∴OD⊥PE,
OH=HD=1,
∵直线AB的解析式为y=-$\frac{1}{2}$x+2,
∴x=1时,y=$\frac{3}{2}$,
∴点P坐标为(1,$\frac{3}{2}$).
故答案为(1,$\frac{3}{2}$).
(2)①如图2中,连接PE交OD于H.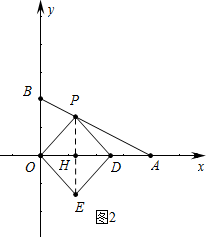
∵四边形OPDE是正方形,不妨设PH=OH=DH=x,
∵PH∥OB,
∴$\frac{PH}{OB}$=$\frac{AH}{AO}$,
∴$\frac{x}{2}$=$\frac{4-x}{4}$,
∴x=$\frac{2}{3}$,
∴OD=2x=$\frac{4}{3}$,
∴D($\frac{4}{3}$,0).
故答案为D($\frac{4}{3}$,0).
②如图3中,如图以OD为直径作⊙H,当⊙H与AB相切时,存在唯一位置使得平行四边形OPDE是矩形.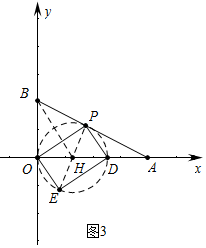
∵AB是⊙H的切线,OB是⊙H的切线,
∴BO=BP=2.
在Rt△AOB中,AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴AP=$\sqrt{5}$-2,
设OH=PH=x,在Rt△APH中,∵AP2+PH2=AH2,
∴($\sqrt{5}$-2)2+x2=(4-x)2,
∴x=$\frac{7+4\sqrt{5}}{8}$,
∴OD=$\frac{7+4\sqrt{5}}{4}$,
∴点D坐标($\frac{7+4\sqrt{5}}{4}$,0).
故答案为($\frac{7+4\sqrt{5}}{4}$,0).
点评 本题考查一次函数综合题.平行四边形的性质和判定、正方形的性质和判定、矩形的性质和判定、圆与直线的位置关系等知识,解题的关键是学会用方程的思想思考问题,学会利用辅助圆解决问题,属于中考压轴题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 亏了10元钱 | B. | 赚了10钱 | C. | 赚了20元钱 | D. | 亏了20元钱 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
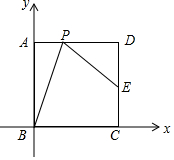 如图,正方形ABCD的边长为2,以点B为原点,BC和AB所在直线分别为x轴和y轴建立平面直角坐标系,点D在第一象限.点E是DC边的中点,P(不与A重合)是AD边上的一动点,设以点P为顶点的抛物线经过点B.
如图,正方形ABCD的边长为2,以点B为原点,BC和AB所在直线分别为x轴和y轴建立平面直角坐标系,点D在第一象限.点E是DC边的中点,P(不与A重合)是AD边上的一动点,设以点P为顶点的抛物线经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -ma-m=-m(a-1) | B. | a2-1=(a-1)2 | C. | a2-6a+9=(a-3)2 | D. | a2+2a+4=(a+2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
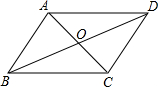 如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )
如图,四边形ABCD的对角线AC,BD相交于点O,欲使ABCD为平行四边形,需添加条件( )| A. | AB=AD,BC=CD | B. | AO=OC,BO=DO | C. | AO⊥OD | D. | AO⊥AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,0) | B. | (-1,-1) | C. | (5,-1) | D. | (-1,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com