
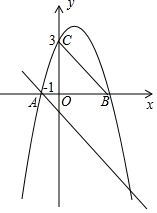
 如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),过点A的直线AD∥BC,交抛物线于另一点D.
如图,二次函数y=ax2+2x+c的图象与x轴交于点A(-1,0)和点B,与y轴交于点C(0,3),过点A的直线AD∥BC,交抛物线于另一点D.分析 (1)把A(-1,0),C(0,3)代入y=ax2+2x+c即可得到结果;
(2)在y=-x2+2x+3中,令y=0,则-x2+2x+3=0,得到B(3,0),由已知条件得直线BC的解析式为y=-x+3,由于AD∥BC,设直线AD的解析式为y=-x+b,即可得到结论;解方程组$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-x-1}\end{array}\right.$得D(4,-5);
(3)①由BC∥AD,得到∠DAB=∠CBA,只要当$\frac{BC}{AD}$=$\frac{PB}{AB}$或$\frac{BC}{AB}$=$\frac{PB}{AD}$时,△PBC∽△ABD,求出AD=5$\sqrt{2}$,AB=4,BC=3$\sqrt{2}$,代入比例式解得BP的长度,即可得到P($\frac{3}{5}$,0)或P(-$\frac{9}{2}$,0).
解答 解:(1)∵次函数y=ax2+2x+c的图象经过点A(-1,0)和点C(0,3),
∴$\left\{\begin{array}{l}{0=a-2+c}\\{3=c}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=-1}\\{c=3}\end{array}\right.$,
∴二次函数的表达式为y=-x2+2x+3;
(2)在y=-x2+2x+3中,令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3,
∴B(3,0),
由已知条件得直线BC的解析式为y=-x+3,
∵AD∥BC,
∴设直线AD的解析式为y=-x+b,
∴0=1+b,
∴b=-1,
∴直线AD的解析式为y=-x-1.
由$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-x-1}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=-5}\end{array}\right.$,
∴D(4,-5);
(3)①∵BC∥AD,
∴∠DAB=∠CBA,
又∵D(4,-5),
∴∠ABD≠45°,点P在点B得到左侧,
∴只可能△ABD∽△BPC或△ABD∽△BCP,
∴$\frac{BC}{AD}$=$\frac{PB}{AB}$或$\frac{BC}{AB}$=$\frac{PB}{AD}$,
∵A(-1,0),B(3,0),C(0,3),D(4,-5),
∵AD=5$\sqrt{2}$,AB=4,BC=3$\sqrt{2}$,
即 $\frac{BP}{4}$=$\frac{3\sqrt{2}}{5\sqrt{2}}$或$\frac{3\sqrt{2}}{4}$=$\frac{BP}{5\sqrt{2}}$,
解得BP=$\frac{12}{5}$或BP=$\frac{15}{2}$,
∵3-$\frac{12}{5}$=$\frac{3}{5}$,3-$\frac{15}{2}$=-$\frac{9}{2}$,
∴P($\frac{3}{5}$,0)或P(-$\frac{9}{2}$,0).
点评 本题主要考查了二次函数解析式的确定、函数图象交点的求法,锐角三角函数,最值的求法,相似三角形的判定和性质,解答(3)题时,要分类讨论,以防漏解或错解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
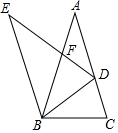 如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.
如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com