
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
【答案】
(1)解:在矩形ABCD中,
∠A=∠D=90°,
AP=1,CD=AB=2,则PB= ![]() ,
,
∴∠ABP+∠APB=90°,
又∵∠BPC=90°,
∴∠APB+∠DPC=90°,
∴∠ABP=∠DPC,
∴△APB∽△DCP,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴PC=2 ![]()
(2)解:①tan∠PEF的值不变.
理由:过F作FG⊥AD,垂足为G,
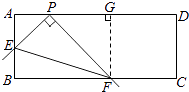
则四边形ABFG是矩形,
∴∠A=∠PGF=90°,GF=AB=2,
∴∠AEP+∠APE=90°,
又∵∠EPF=90°,
∴∠APE+∠GPF=90°,
∴∠AEP=∠GPF,
∴△APE∽△GPF,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴Rt△EPF中,tan∠PEF= ![]() =2,
=2,
∴tan∠PEF的值不变;
②设线段EF的中点为O,连接OP,OB,
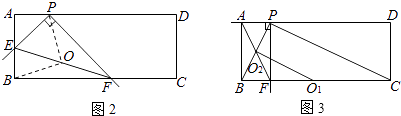
∵在Rt△EPF中,OP= ![]() EF,
EF,
在Rt△EBF中,OB= ![]() EF,
EF,
∴OP=OB= ![]() EF,
EF,
∴O点在线段BP的垂直平分线上,
∴线段EF的中点经过的路线长为O1O2= ![]() PC=
PC= ![]()
【解析】1)由勾股定理求PB,利用互余关系证明△APB∽△DCP,利用相似比求PC;
(2)①tan∠PEF的值不变.过F作FG⊥AD,垂足为G,同(1)的方法证明△APB∽△DCP,得相似比,再利用锐角三角函数的定义求值;
②如图3,画出起始位置和终点位置时,线段EF的中点O1,O2,连接O1O2,线段O1O2即为线段EF的中点经过的路线长,也就是△BPC的中位线.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉揭示了二项和![]() 的展开式的各项系数规律,比欧洲的发现早三百年,为纪念杨辉的功绩,世人称如图中右图叫“杨辉三角”。
的展开式的各项系数规律,比欧洲的发现早三百年,为纪念杨辉的功绩,世人称如图中右图叫“杨辉三角”。
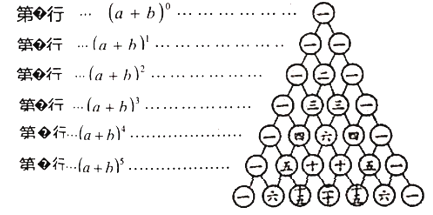
(1)观察“杨辉三角”规律,依次写出“杨辉三角”第![]() 行中从左到右的各数;
行中从左到右的各数;
(2)请运用幂的意义和多项式乘法法则,按如下要求展开下列各式,以验证“杨辉三角”第四行的规律:展开后各项按字母![]() 降幂、
降幂、![]() 升幂排列
升幂排列![]()
(3)解不等式![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )

A. 70°B. 65°C. 55°D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,……,已知正方形ABCD的面积为S1为1,按上述方法所作的正方形的面积依次为S2,S3,……………,则Sn(n为正整数),那么第n个正方形的面积Sn等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
A.45°
B.85°
C.90°
D.95°
查看答案和解析>>
科目:初中数学 来源: 题型:
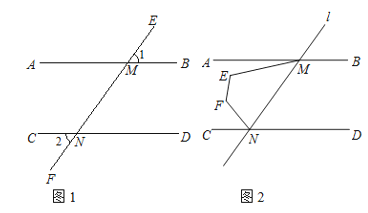
【题目】如图,直线l分别交AB,CD于点M,N(点M在点N的右侧),若∠1=∠2
(1)求证:AB//CD;
(2)如图,点E、F在AB,CD之间,且在MN的左侧,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度数;
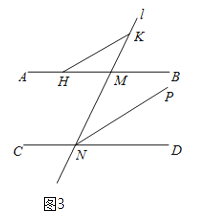
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接写出∠PND和∠QHB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.


(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 为
为![]() 的中点,分别连接
的中点,分别连接![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() 的面积为30,
的面积为30,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com