
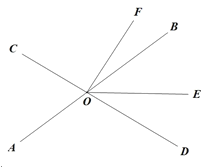
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]()
(1)与![]() 互余的角;
互余的角;
(2)求![]() 的度数.
的度数.
【答案】(1)![]() 或
或![]() ,(2)
,(2)![]()
【解析】
(1)由垂直的定义可得∠BOF+∠BOD=90°,再由∠BOD=∠AOC,可得∠BOF+∠AOC=90°,由此即可得答案;
(2)根据对顶角相等以及垂直的定义可求出∠BOF=90°-72°=18°,再由OE平分∠BOD,得出∠BOE的度数,继而可求得答案.
(1)∵OF⊥CD,
∴∠FOD=90°,
∴∠BOF+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠BOF+∠AOC=90°,
∴与∠BOF互余的角为∠BOD或∠AOC;
(2)∵直线AB和CD相交于点O,
∴∠BOD=∠AOC=72°,
∵OF⊥CD,
∴∠BOF=90°-72°=18°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=36°,
∠BOD=36°,
∴∠EOF=36°+18°=54°.


科目:初中数学 来源: 题型:
【题目】
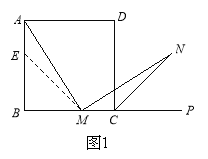
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
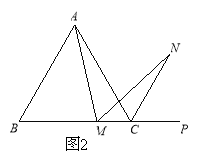
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随即抽查部分同学体育测试成绩(由高到低分四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图:
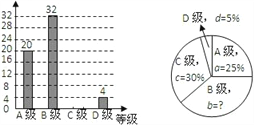
请根据以上不完整的统计图提供的信息,解答下列问题:
(1) 该课题研究小组共抽查了_________名同学的体育测试成绩,扇形统计图中B级所占的百分比b=__________
(2) 补全条形统计图.
(3) 若该校九年级共有200名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)均有___________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县“果菜大王”王大炮收货番茄20吨,青椒12吨.现计划租用甲、乙两种货车共8辆将这批果菜全部运往外地销售,已知一辆甲种货车可装番茄4吨和青椒1吨,一辆乙种货车可装番茄和青椒各2吨.
(1)王灿有几种方案安排甲、乙两种货车可一次性地将果菜运到销售地?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王大炮应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别沿同一条路线从
,甲、乙两车分别沿同一条路线从![]() 地出发驶往
地出发驶往![]() 地,已知甲车的速度为
地,已知甲车的速度为![]() ,乙车的速度为
,乙车的速度为![]() ,甲车先出发
,甲车先出发![]() 后乙车再出发,乙车到达
后乙车再出发,乙车到达![]() 地后再原地等甲车.
地后再原地等甲车.
(1)求乙车出发多长时间追上甲车?
(2)求乙车出发多长时间与甲车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图.
(1)在![]() 的内部任取一个点E,过点E作EM⊥OB;
的内部任取一个点E,过点E作EM⊥OB;
(2)在边![]() 上取一点N,作NF⊥OA于点N,且NF=EM;
上取一点N,作NF⊥OA于点N,且NF=EM;
(3)过点E作直线l1∥OB,过点F作直线l2∥OA,l1 与l2交于点![]() ;
;
(4)画射线![]() .
.
则射线![]() 为
为![]() 的平分线.
的平分线.

根据小明的画法回答下面的问题:
(1)小明作l1∥OB,l2∥OA的目的是___________________________________________;
(2)l1 与l2交于点![]() ,则射线
,则射线![]() 为
为![]() 的平分线的依据是__________________________.
的平分线的依据是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B , C重合),过M作MN∥ ![]() 轴交抛物线于N , 若点M的横坐标为
轴交抛物线于N , 若点M的横坐标为 ![]() ,请用含
,请用含 ![]() 的代数式表示线段MN的长。
的代数式表示线段MN的长。
(4)在(3)的条件下,连接NB、NC , 则是否存在点M,使△BNC的面积最大?若存在,求 ![]() 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com