
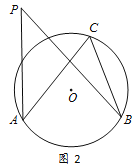
ЎѕМвДїЎїИзНј1Ј¬µгAЎўBЎўC·Ц±рКЗЎСOЙПІ»ЦШєПµДИэµгЈ¬Б¬ЅУACЎўBC.
ЈЁ1Ј©ИзНј2Ј¬µгPКЗЦ±ПЯABЙП·ЅЗТФЪЎСOНвµДИОТвТ»µгЈ¬ Б¬ЅУAPЎўBP.КФ±ИЅПЎПAPBУлЎПACBµДґуРЎ№ШПµЈ¬ІўЛµГчАнУЙЈ»
ЈЁ2Ј© ИфµгPКЗЎСOДЪИОТвТ»µгЈ¬ Б¬ЅУAPЎўBPЈ¬±ИЅПЎПAPBУлЎПACBґуРЎ№ШПµЈ»
ЈЁ3Ј©ИзНј3Ј¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬µгAУлµгBµДЧш±к·Ц±рКЗЈЁ1Ј¬0Ј©Ј¬ЈЁ5Ј¬0Ј©Ј¬µгPКЗЦ±ПЯyЈЅЈxЙПТ»¶ЇµгЈ¬µ±ЎПAPBИЎµГЧоґуЦµК±Ј¬Ц±ЅУРґіцµгPµДЧш±кЈ¬ІўјтТЄЛµГчµгPµДО»ЦГКЗИзєОИ·¶ЁµДЈ®


Ўѕґр°ёЎїЈЁ1Ј©ЎПAPBЈјЎПACBЈ»ЈЁ2Ј©ЎПAPBЈѕЎПACBЈ»ЈЁ3Ј©![]() .
.
ЎѕЅвОцЎї
ЈЁ1Ј©ЙиAPУлЎСOЅ»УЪµгEЈ¬Б¬ЅУAEЈ¬ёщѕЭФІЦЬЅЗ¶ЁАнїЙЦЄЎПAEB=ЎПACBЈ¬ФЩУЙИэЅЗРОНвЅЗµДРФЦКїЙµГЎПAEBЈѕЎПAPBЈ¬УЙґЛїЙµГіцЅбВЫЈ»
ЈЁ2Ј©ЙиBPµДСУі¤ПЯУлЎСOЅ»УЪµгDЈ¬Б¬ЅУADЈ¬ёщѕЭФІЦЬЅЗ¶ЁАнїЙЦЄЎПD=ЎПCЈ¬ФЩУЙИэЅЗРОНвЅЗµДРФЦКїЙµГЎПDЈјЎПAPBЈ¬УЙґЛїЙµГіцЅбВЫЈ»
ЈЁ3Ј©УЙИэЅЗРОНвЅЗµДРФЦКїЙЦ¤µГЈєФЪН¬ФІ»тµИФІЦРЈ¬Н¬»ЎЛщ¶ФµДФІЦЬЅЗґуУЪН¬»ЎЛщ¶ФµДФІНвЅЗЈ®ТЄЎПAPBЧоґуЈ¬Ц»Ри№№Фм№эµгAЎўµгBЗТУлЦ±ПЯyЈЅЈxПаЗРµДФІЈ¬ЗРµгѕНКЗК№µГЎПAPBЧоґуµДµгPЈ¬И»єуЅбєПЗРПЯµДРФЦКЎўИэЅЗРОНвЅЗµДРФЦКЎў№ґ№Й¶ЁАнµИЦЄК¶јґїЙЅвѕцОКМвЈ®
ЈЁ1Ј©ЎПAPBЈјЎПACB
ИзНјЈ¬І»·БЙиPBЅ»ABЙП·ЅФІ»ЎУЪµгEЈ¬Б¬ЅУAE.
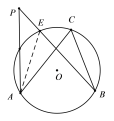
ЎЯ ЎПAEBКЗЎчPAEµДНвЅЗ
Ўа ЎПAEBЈѕЎПAPB
УЦЎЯ ЎПAEB=ЎПACB
Ўа ЎПAPBЈјЎПACB
ЈЁ2Ј©ЎПAPBЈѕЎПACBЈ¬
ФЪНјЦРЈ¬СУі¤BPЅ»ФІУЪµгDЈ¬Б¬ЅУADЈ®
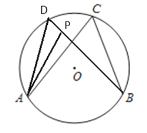
ЎЯЎПD=ЎПCЈ¬
УЦЎЯЎПDЈјЎПAPBЈ¬
ЎаЎПAPBЈѕЎПACBЈ®
ЈЁ3Ј©![]() ,
,
ФЪПЯ¶ОABµДґ№Ц±ЖЅ·ЦПЯЙПХТТ»µгQЈ¬µ±ТФµгQОЄФІРДЎўQAОЄ°лѕ¶µДФІУлЦ±ПЯy=ЈxПаЗРУЪµЪЛДПуПЮК±Ј¬ФтЗРµгјґОЄЛщТЄИ·¶ЁµДµгPµДО»ЦГ.
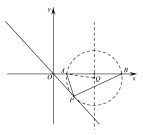
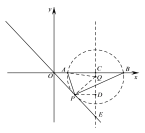
ИзНјЈ¬ЎСQЗРЦ±ПЯУЪµгPЈ¬ЧчABµДґ№Ц±ЖЅ·ЦПЯCQ.
ЙиCQµДі¤ОЄxЈ¬УЙМхјюїЙЦЄЈєOA=1Ј¬OC=CE=3Ј¬
ФтQE=3ЈxЈ¬QD=![]() Ј¬
Ј¬
Ўа![]()
RtЎчAQCЦРЈ¬![]() ,
,
Ўа![]() ,
,
ЅвµГЈє![]() Ј¬ПФИ»µгPФЪµЪЛДПуПЮ±ИФЪµЪ¶юПуПЮК±ЎПAPBёьґу,
Ј¬ПФИ»µгPФЪµЪЛДПуПЮ±ИФЪµЪ¶юПуПЮК±ЎПAPBёьґу,
Ўа![]() ,
,
Ўа![]() ,
,
ЎаP![]() .
.


 МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё
МмМмПтЙПТ»±ѕєГѕнПµБРґр°ё РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
РЎС§Йъ10·ЦЦУУ¦УГМвПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
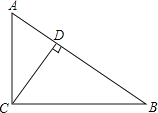
ЎѕМвДїЎїИзНј,ФЪRtЎчABCЦР,ЎПACB=90,CDЎНAB,ґ№ЧгОЄD,tanЎПACD=![]() Ј¬AB=5Ј¬ДЗГґCDµДі¤КЗ_____.
Ј¬AB=5Ј¬ДЗГґCDµДі¤КЗ_____.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЛщКѕЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ЎчABCµД¶ҐµгЧш±к·Ц±рКЗAЈЁ-2Ј¬3Ј©Ј¬BЈЁm-1Ј¬1Ј©Ј¬CЈЁ1Ј¬-2Ј©Ј¬µгB№ШУЪxЦбµД¶ФіЖµгPµДЧш±кОЄЈЁ-3Ј¬n-2Ј©Ј®
ЈЁ1Ј©ЗуmЈ¬nµДЦµЈ»
ЈЁ2Ј©»іцЎчABCЈ¬ІўЗуіцЛьµДГж»эЈ»
ЈЁ3Ј©»іцУлЎчABC№ШУЪyЦбіЙЦб¶ФіЖµДНјРОЎчA1B1C1Ј¬ІўРґіцЎчA1B1C1Ј¬ёчёц¶ҐµгµДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪRtЎчABCЦРЈ¬ЎПA=90ЎгЈ¬УРТ»ёцИсЅЗОЄ60ЎгЈ¬BC=6Ј®ИфµгPФЪЦ±ПЯACЙПЈЁІ»УлµгAЈ¬CЦШєПЈ©Ј¬ЗТЎПABP=30ЎгЈ¬ФтCPµДі¤ОЄЎЎ ЎЎЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЈЁ1Ј©(x+1)2-3=0Ј» ЈЁ2Ј©2x2-3=5xЈ»
ЈЁ3Ј©3x2-6x+2=0 Ј» ЈЁ4Ј©9(x-2)2-4x2=0.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЈЁМЅѕїУлЦ¤ГчЈ©
ФЪХэ·ЅРОABCDЦРЈ¬GКЗЙдПЯACЙПТ»¶ЇµгЈЁІ»УлµгAЎўCЦШєПЈ©Ј¬Б¬BGЈ¬ЧчBHЎНBGЈ¬ЗТК№BHЈЅBGЈ¬Б¬GHЎўCHЈ®
ЈЁ1Ј©ИфGФЪACЙПЈЁИзНј1Ј©Ј¬ФтЈєўЩНјЦРУлЎчABGИ«µИµДИэЅЗРОКЗЎЎ ЎЎЈ®
ўЪПЯ¶ОAGЎўCGЎўGHЦ®јдµДКэБї№ШПµКЗЎЎ ЎЎЈ®
ЈЁ2Ј©ИфGФЪACµДСУі¤ПЯЙПЈЁИзНј2Ј©Ј¬ДЗГґПЯ¶ОAGЎўCGЎўBGЦ®јдУРФхСщµДКэБї№ШПµЈїРґіцЅбВЫІўёшіцЦ¤ГчЈ»
ЈЁУ¦УГЈ©ЈЁ3Ј©ИзНј3Ј¬GФЪХэ·ЅРОABCDµД¶ФЅЗПЯCAµДСУі¤ПЯЙПЈ¬ТФBGОЄ±ЯЧчХэ·ЅРОBGMNЈ¬ИфAGЈЅ2Ј¬ADЈЅ4Ј¬ЗлЦ±ЅУРґіцХэ·ЅРОBGMNµДГж»эЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіІї¶УЅ«ФЪЦё¶ЁЙЅЗшЅшРРѕьКВСЭП°Ј¬ОЄБЛК№µАВ·±гУЪІї¶УЦШРНіµБѕНЁ№эЈ¬Ії¶У№¤±шБ¬ЅУµЅЗАРЮТ»¶Оі¤3600ГЧµАВ·µДИООсЈ¬°ґФјЖ»®НкіЙЧЬИООсµД![]() єуЈ¬ОЄБЛИГµАВ·ѕЎїмН¶ИлК№УГЈ¬№¤±шБ¬Ѕ«№¤ЧчР§ВКМбёЯБЛ50%Ј¬Т»№ІУГБЛ10РЎК±НкіЙИООсЈ®
єуЈ¬ОЄБЛИГµАВ·ѕЎїмН¶ИлК№УГЈ¬№¤±шБ¬Ѕ«№¤ЧчР§ВКМбёЯБЛ50%Ј¬Т»№ІУГБЛ10РЎК±НкіЙИООсЈ®
ЈЁ1Ј©°ґФјЖ»®НкіЙЧЬИООсµД![]() К±Ј¬ТСЗАРЮµАВ·ЎЎ ЎЎГЧЈ»
К±Ј¬ТСЗАРЮµАВ·ЎЎ ЎЎГЧЈ»
ЈЁ2Ј©ЗуФјЖ»®ГїРЎК±ЗАРЮµАВ·¶аЙЩГЧЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЎчABNєНЎчACMО»ЦГИзНјЛщКѕЈ¬AB=ACЈ¬AD=AEЈ¬ЎП1=ЎП2Ј®
ЈЁ1Ј©ЗуЦ¤ЈєBD=CEЈ»
ЈЁ2Ј©ЗуЦ¤ЈєЎПM=ЎПNЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
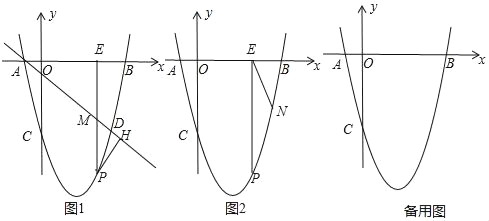
ЎѕМвДїЎїИзНј1Ј¬ФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ЕЧОпПЯy=ax2+bx+cЈЁaЎЩ0Ј©УлxЦбЅ»УЪAЈ¬BБЅµгЈЁµгAФЪµгBµДЧуІаЈ©Ј¬УлyЦбЅ»УЪµгCЈ¬µгAµДЧш±кОЄЈЁ©Ѓ1Ј¬0Ј©Ј¬ЗТOC=OBЈ¬tanЎПOAC=4Ј®
ЈЁ1Ј©ЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©ИфµгDєНµгC№ШУЪЕЧОпПЯµД¶ФіЖЦб¶ФіЖЈ¬Ц±ПЯADПВ·ЅµДЕЧОпПЯЙПУРТ»µгPЈ¬№эµгPЧчPHЎНADУЪµгHЈ¬ЧчPMЖЅРРУЪyЦбЅ»Ц±ПЯADУЪµгMЈ¬Ѕ»xЦбУЪµгEЈ¬ЗуЎчPHMµДЦЬі¤µДЧоґуЦµЈ®
ЈЁ3Ј©ФЪЈЁ2Ј©µДМхјюПВЈ¬ИзНј2Ј¬ФЪЦ±ПЯEPµДУТІаЎўxЦбПВ·ЅµДЕЧОпПЯЙПКЗ·сґжФЪµгNЈ¬№эµгNЧчNGЎНxЦбЅ»xЦбУЪµгGЈ¬К№µГТФµгEЎўNЎўGОЄ¶ҐµгµДИэЅЗРОУлЎчAOCПаЛЖЈїИз№ыґжФЪЈ¬ЗлЦ±ЅУРґіцµгGµДЧш±кЈєИз№ыІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com