�����1��֤������OD��AH��
���OAP=��DAC=90��-��AOD��
������OABC�У�OA=OC=4����AOP=��OCD=90�㣬����
��
| | OA=OC | | ��OAP=��COD | | ��AOP=��OCD |
| |
��
���AOP�ա�OCD
��OP=CD��
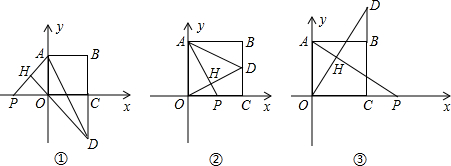
��2���⣺�ٵ�P��x�Ḻ������ʱ��P��t��0������t��0����ͼ�٣�
����Rt��AOP��OH��AP��
���POH=��PAO=90��-��APO��
�֡ߡ�POH=��COD��
���COD=��PAO��
�ڡ�AOP���OCD�У�
��
| | OA=OC | | ��PAO=��COD | | ��AOP=��OCD |
| |
��
���AOP�ա�OCD��
��OP=CD=-t����BD=BC+CD=4-t��
����AOP����A��B��DΪ��������������ƣ����У�
=
���ã�
=
��ã�t=2-2
��t=2+2
����ֵ��ȥ����
�ڵ���P���߶�OC��ʱ��P��t��0����0��t��4����ͼ�ڣ�
��ΪOP��OA��BD��AB��OA=AB��
����AOP����A��B��DΪ��������������ƣ���ô�У�
=
������OP=BD������
t=4-t��t=2��
�۵���P�ڵ�C�Ҳ�ʱ��P��t��0����t��4����ͼ�ۣ�
ͬ�ٿ����t=2+2
��
���ϣ�t
1=2��t
2=
2+2��t
3=
2-2��
��3���⣺������ڷ��������ĵ�Q��������������ۣ�
��PCΪƽ���ı��εĶԽ��ߣ���QP��CD����QP=CD��
��P��t��0����D��4��t������Q��t��-t��������������y=-
x
2+
x+4�У��ã�
-
t
2+
t+4=-t������t
2-10t-24=0��
��ã�t
1=-2��t
2=12��
��PCΪƽ���ı��εıߣ���DQ��PC����AD=PC��
��P��t��0����D��4��t������ PC=QD=|t-4|��Q��t��t����8-t��t����
Q��t��t��ʱ��t=-
t
2+
t+4������t
2+2t-24=0��
��� t
1=4���ᣩ��t
2=-6��
Q��8-t��t��ʱ��t=-
��8-t��
2+
��8-t��+4������t
2-6t+8=0��
��� t
1=4���ᣩ��t
2=2��
���Ͽ�֪��t
1=2��t
2=12��t
3=-6��t
4=-2��
����ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ�


 ��2���⣺�ٵ�P��x�Ḻ������ʱ��P��t��0������t��0����ͼ�٣�
��2���⣺�ٵ�P��x�Ḻ������ʱ��P��t��0������t��0����ͼ�٣�


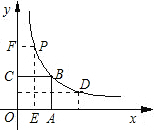 ��ͼ����֪��������OABC�����Ϊ9����OΪ����ԭ�㣬��A��x���ϣ���C��y���ϣ���B�ں���y=
��ͼ����֪��������OABC�����Ϊ9����OΪ����ԭ�㣬��A��x���ϣ���C��y���ϣ���B�ں���y=
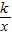 ��k��0��x��0����ͼ���ϣ���P��m��n���Ǻ���y=
��k��0��x��0����ͼ���ϣ���P��m��n���Ǻ���y= ��k��0��x��0����ͼ���ϵ�����һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF�к�������OABC���غϲ��ֵ����ΪS��
��k��0��x��0����ͼ���ϵ�����һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF�к�������OABC���غϲ��ֵ����ΪS�� ʱ����P�����꣮
ʱ����P�����꣮
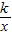 ��k��0��x��0����ͼ���ϣ���P��m��n���Ǻ���y=
��k��0��x��0����ͼ���ϣ���P��m��n���Ǻ���y= ��k��0��x��0����ͼ���ϵ�����һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF�к�������OABC���غϲ��ֵ����ΪS��
��k��0��x��0����ͼ���ϵ�����һ�㣬����P�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF�к�������OABC���غϲ��ֵ����ΪS�� ʱ����P�����꣮
ʱ����P�����꣮