
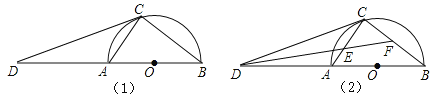
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.
【答案】(1)见解析;(2)45°.
【解析】试题分析:(1)连接OC,根据切线的性质和直径所对的圆周角是直角得出∠DCO=∠ACB=90°,然后根据等角的余角相等即可得出结论;
(2)根据三角形的外角的性质证明∠CEF=∠CFE即可求解.
试题解析:
(1)证明:如图1中,连接OC.
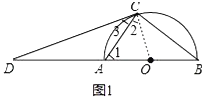
∵OA=OC,∴∠1=∠2,
∵CD是⊙O切线,∴OC⊥CD,
∴∠DCO=90°,∴∠3+∠2=90°,
∵AB是直径,∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,∴∠CEF=∠CFE,
∵∠ECF=90°,
∴∠CEF=∠CFE=45°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A为一数,且A=25×76×114 , 则下列选项中所表示的数,何者是A的因子?( )
A.24×5
B.77×113
C.24×74×114
D.26×76×116
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为![]() ,所以
,所以![]() 就有最小值1,即
就有最小值1,即![]() ,只有当
,只有当![]() 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为![]() ,所以
,所以![]() 有最大值1,即
有最大值1,即![]() ,只有在
,只有在![]() 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.
(1)当![]() =_______时,代数式3(x+3)2+4有最_______(填写大或小)值为___________.
=_______时,代数式3(x+3)2+4有最_______(填写大或小)值为___________.
(2)当![]() =_______时,代数式-2x2+4x+3有最_______(填写大或小)值为__________.
=_______时,代数式-2x2+4x+3有最_______(填写大或小)值为__________.
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com