
【题目】如图,已知点E,F分别是ABCD的边BC,AD上的中点,且∠BAC=90°. 
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
在Rt△ABC中,∠BAC=90°,点E是BC边的中点,
∴AE= ![]() BC=CE,
BC=CE,
同理,AF= ![]() AD=CF,
AD=CF,
∴AE=CE=AF=CF,
∴四边形AECF是菱形
(2)解:连接EF交AC于点O,如图所示:
在Rt△ABC中,∠BAC=90°,∠B=30°,BC=10,
∴AC= ![]() BC=5,AB=
BC=5,AB= ![]() AC=5
AC=5 ![]() ,
,
∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,
∴OE是△ABC的中位线,
∴OE= ![]() AB=
AB= ![]() ,
,
∴EF=5 ![]() ,
,
∴菱形AECF的面积= ![]() ACEF=
ACEF= ![]() ×5×5
×5×5 ![]() =
= ![]() .
.

【解析】(1)由平行四边形的性质得出AD=BC,由直角三角形斜边上的中线性质得出AE= ![]() BC=CE,AF=
BC=CE,AF= ![]() AD=CF,得出AE=CE=AF=CF,即可得出结论;(2)连接EF交AC于点O,解直角三角形求出AC、AB,由三角形中位线定理求出OE,得出EF,菱形AECF的面积=
AD=CF,得出AE=CE=AF=CF,即可得出结论;(2)连接EF交AC于点O,解直角三角形求出AC、AB,由三角形中位线定理求出OE,得出EF,菱形AECF的面积= ![]() ACEF,即可得出结果.
ACEF,即可得出结果.


科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 周长记作C1;再作第二个正方形A2B2C2A3 , 周长记作C2;继续作第三个正方形A3B3C3A4 , 周长记作C3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Cn= . 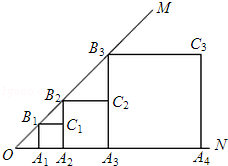
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
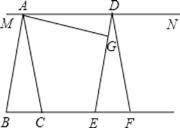
【题目】如图所示,将![]() 沿直线BC方向平移
沿直线BC方向平移![]() 的位置,G是DE上一点,连接AG,过点A、D作直线MN.
的位置,G是DE上一点,连接AG,过点A、D作直线MN.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断AG与DE的位置关系,并证明你的结论.
,判断AG与DE的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作![]() ,与AC、DC分别交于点
,与AC、DC分别交于点![]() 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、![]() 下列结论:
下列结论: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,则
,则![]() 其中结论正确的有
其中结论正确的有![]()
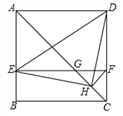
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com