
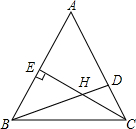
 如图,在△ABC中,∠ABC=50°,∠ACB=70°,BD是∠ABC的平分线,CE是AB边上的高线,BD与CE交于点H,求∠ADB和∠BHC的度数.
如图,在△ABC中,∠ABC=50°,∠ACB=70°,BD是∠ABC的平分线,CE是AB边上的高线,BD与CE交于点H,求∠ADB和∠BHC的度数. 分析 先根据三角形内角和定理求出∠A的度数,再由角平分线的性质得出∠ABD的度数,进而可得出∠ADB的度数;由三角形外角的性质可得出∠BHC的度数.
解答 解:∵在△ABC中,∠ABC=50°,∠ACB=70°,
∴∠A=180°-50°-70°=60°.
∵BD是∠ABC的平分线,
∴∠ABD=$\frac{1}{2}$∠ABC=25°,
∴∠ADB=180°-∠A-∠ABD=180°-60°-25°=95°;
∵CE是AB边上的高线,
∴∠BEH=90°,
∴∠BHC=∠BEH+∠ABD=90°+25°=115°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是一施工队建房时挖地基的平面图,按标准应为长方形,挖完后,技术人员经测量发现AB=DC=12m,AD=BC=5m,AC=14m,请你帮忙检验一下挖的是否合格?
如图,是一施工队建房时挖地基的平面图,按标准应为长方形,挖完后,技术人员经测量发现AB=DC=12m,AD=BC=5m,AC=14m,请你帮忙检验一下挖的是否合格?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com