
【题目】关于x的分式方程![]() =1的解是正数,则m的取值范围是_____.
=1的解是正数,则m的取值范围是_____.
【答案】m<1
【解析】试题分析:去分母得:2x+m=x-2,
解得:x=-m-2,
∵关于x的方程![]() =1的解是正数,
=1的解是正数,
∴-m-2>0,
解得m<-2,
又∵x=-m-2≠2,
∴m≠-4,
∴m的取值范围是:m<-2且m≠-4.
故答案为:m<-2且m≠-4.
点睛:此题主要考查了分式方程的解,要熟练掌握,解答此题的关键是要明确:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.
【题型】填空题
【结束】
18
【题目】若关于x的分式方程 ![]() 无解,则m的值为_______.
无解,则m的值为_______.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y= ![]() 的图象的两个交点.
的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出方程kx+b﹣ ![]() =0的解;
=0的解;
(3)求△AOB的面积;
(4)观察图象,直接写出不等式kx+b﹣ ![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F.如图1,当点P与点O重合时,显然有DF=CF.
(1)如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E.
①求证:DF=EF;
②写出线段PC、PA、CE之间的一个等量关系;并说出理由;
(2)若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD于点E.请完成图3并判断(1)中的结论①、②是否分别成立?若不成立,写出相应的结论.(所写结论均不必证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 , 乙成绩的平均数是;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ; (4)
; (4) ![]()
【解析】试题分析:(1)分子、分母分解因式后约分即可;
(2)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可;
(3)第二个分式分子、分母分解因式后约分,然后通分转化为同分母分式,最后依照同分母分式的加减法则计算即可;
(4)先通分计算括号内分式的减法,然后把除法转化为乘法,分子、分母分解因式后约分即可.
试题解析:
解:(1)原式=
=![]() ;
;
(2)原式=![]()
=![]()
=![]() ;
;
(3)原式=![]()
=![]()
=![]()
=![]()
=![]() ;
;
(4)原式=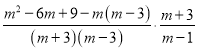
=![]()
=![]() .
.
点睛:此题考查了分式的混合运算,熟练掌握运算法则和运算顺序是解本题的关键.
【题型】解答题
【结束】
20
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )

A. 扇形甲的圆心角是72° B. 学生的总人数是90人
C. 初三的人数比初二的人数多10人 D. 初一的人数比初三的人数少15人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好的治理水质,保护环境,市治污办事处预购买10台污水处理设备,现有A、B两种型号的设备,其中价格及污水处理量如下表:
A型 | B型 | |
价格(万元) | a | b |
处理污水量(吨/月) | 240 | 200 |
询问商家得知:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元,根据以上条件.
(1)求a、b的值;
(2)市污水处理办公室由于资金缺乏,购买污水处理设备的资金最多105万元,你认为该有几种购买方案?
(3)在(2)的情况下,若每月污水处理量要求不低于2040吨,为节约资金,请你帮污水处理办事处选取一种最省钱的方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com