
分析 先由2015=5×13×31,进而得出d值为1、5、13、31、65、155、403、2015,再根据个位数字的乘方的特点分类确定出个位数字,最后找出最大的即可.
解答 解:∵2015=5×13×31,
∴2015=1×2015=5×403=13×155=31×65,
∵d为2015的正因数,
∴2015有8个正因数,
用G(n)表示n的个位数字,
∴G(12015)=G(3165)=1,
G(20151)=G(5403)=G(6531)=G(15513)=5,
G(13155)=G(3155)=G(34×38+3)=G(33)=7,
G(4035)=G(35)=3,
从而,${d^{\frac{2015}{d}}}$的个位数字的最大值7;
故答案为7.
点评 此题是尾数特征题目,主要考查了分解因数,整数的乘方的个位数字的确定方法,确定找出2015的八个因数对应的幂的个数数字是解本题的关键.


科目:初中数学 来源: 题型:解答题
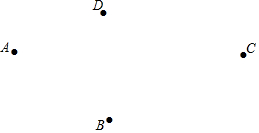 如图,在同一平面内四个点A,B,C,D.
如图,在同一平面内四个点A,B,C,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
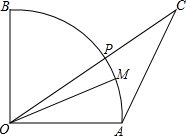 如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )| A. | 4 | B. | 2 | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
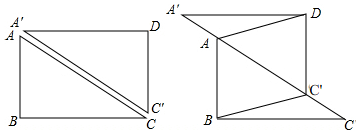
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
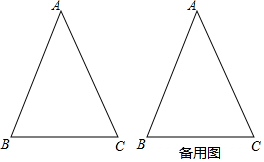
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
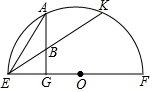 如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若EB=2,EK=6,则AE=2$\sqrt{3}$.
如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若EB=2,EK=6,则AE=2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com