
【题目】如图,在△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).

A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】B
【解析】连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD-C′D计算即可得解.
如图,连接BB′,

∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,
∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴AB=BB′,
在△ABC′和△B′BC′中,
 ,
,
∴△ABC′≌△B′BC′(SSS),
∴∠ABC′=∠B′BC′,
延长BC′交AB′于D,
则BD⊥AB′,
∵∠C=90°,AC=BC=![]() ,
,
∴AB=![]() =2,
=2,
∴BD=2×![]() =
=![]() ,
,
C′D=![]() ×2=1,
×2=1,
∴BC′=BD-C′D=![]() -1.
-1.
故选:B.


科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.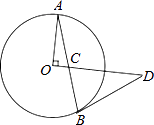
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4![]() x+12+m=0.
x+12+m=0.
(1)若方程的一个根是![]() ,求m的值及方程的另一根;
,求m的值及方程的另一根;
(2)若方程的两根恰为等腰三角形的两腰,而这个三角形的底边为m,求m的值及这个等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题共10分)水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
(3)现需按毛利润的10%交纳各种税费,人工费每日按销售量每千克支出0.9元,水电房租费每日102元,若剩下的每天总纯利润要达到5100元,则每千克涨价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在横线上和括号内填上推导内容或依据.
如图,已知 ![]() ,
, ![]() ,求证:
,求证: ![]() .
.
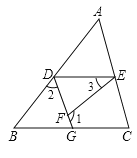
证明: ![]() (已知),
(已知),
![]() ( ),
( ),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
∵![]() (已知),
(已知),
![]() ( ).
( ).
![]() ( ).
( ).
![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,若存在一个内角角度,是另外一个内角角度的
中,若存在一个内角角度,是另外一个内角角度的![]() 倍(
倍(![]() 为大于1的正整数),则称
为大于1的正整数),则称![]() 为
为![]() 倍角三角形.例如,在
倍角三角形.例如,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,所以
,所以![]() 为3倍角三角形.
为3倍角三角形.
(1)在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 为________倍角三角形;
为________倍角三角形;
(2)若![]() 是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的
是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的![]() ,求
,求![]() 的最小内角.
的最小内角.
(3)若![]() 是2倍角三角形,且
是2倍角三角形,且![]() ,请直接写出
,请直接写出![]() 的最小内角的取值范围.
的最小内角的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com