
【题目】![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)证明见解析;(2)∠EBD=140°.
【解析】
(1)根据同角的余角相等可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,根据全等三角形的性质即可得结论;(2)延长DB,交AE与F,交EC于G,由(1)得△BCD≌△ACE,可得∠AEC=∠BDC,根据对顶角相等可得∠EFD=∠ECD=90°,利用外角性质求出∠EBD的度数即可.
(1)∵![]() ,
,
∴∠BCD+∠BCE=∠ACE+∠BCE,
∴∠BCD=∠ACE,
在△BCD和△ACE中,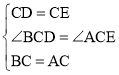 ,
,
∴△BCD≌△ACE,
∴BD=AE.
(2)延长DB,交AE与F,交EC于G,
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∵∠DGC=∠EGF,∠ECD=90°,
∴∠EFD=∠ECD=90°,
∵∠AEB=50°,
∴∠EBD=∠EFD+∠AEB=90°+50°=140°.


科目:初中数学 来源: 题型:
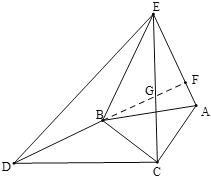
【题目】广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完.销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示.下列结论正确的是( )

A.降价后西瓜的单价为2元/千克B.广宇一共进了50千克西瓜
C.售完西瓜后广宇获得的总利润为44元D.降价前的单价比降价后的单价多0.6元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图1);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图2);再展平纸片(如图3),则图3中∠α的大小为()
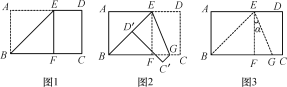
A.30°B.25.5°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
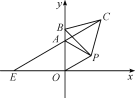
【题目】如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点B为y轴上一动点,以BP为边作等边△PBC,延长CA交x轴于点E.
(1)求证:OB=AC;
(2)∠CAP的度数是;
(3)当B点运动时,猜想AE的长度是否发生变化?并说明理由;
(4)在(3)的条件下,在y轴上存在点Q,使得△AEQ为等腰三角形,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从![]() ,
,![]() 两地去同一城市
两地去同一城市![]() ,它们离
,它们离![]() 地的路程随时间变化的图象如图所示,根据图象中的信息解答以下问题:
地的路程随时间变化的图象如图所示,根据图象中的信息解答以下问题:

(1)![]() ,
,![]() 两地相距______
两地相距______![]() ;
;
(2)分别求出摩托车和汽车的行驶速度;
(3)若两图象的交点为![]() ,求点
,求点![]() 的坐标,并指出点
的坐标,并指出点![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售员的奖励工资由两部分组成:基本工资,每人每月2400元;奖励工资,每销售一件产品,奖励10元.
(1)设某销售员月销售产品![]() 件,他应得的工资为
件,他应得的工资为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若该销售员某月工资为3600元,他这个月销价了多少件产品?
(3)要使月工资超过4200元,该月的销售量应当超过多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com