练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．化简：-3x2y+2xy2+3xy2-2x2y．

    分析 把同类项的系数相加，所得结果作为系数，字母和字母的指数不变，即可得结果．

    解答 解：-3x2y+2xy2+3xy2-2x2y
    =（-3-2）x2y+（2+3）xy2
    =-5x2y+5xy2．

    点评 本题主要考查了合并同类项的运算法则，掌握同类项的概念，会辨别同类项，运用法则是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．已知BC=CD，∠BCD=90°，CE=CF，图中有全等三角形吗？如果有，请证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知a=$\frac{1}{2}$（$\sqrt{2013}$+$\sqrt{2011}$），b=$\frac{1}{2}$（$\sqrt{2013}$-$\sqrt{2011}$），求a2b-ab2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

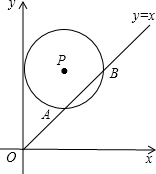    20．如图，在平面直角坐标系中，与y轴相切的⊙P的圆心是（2，a）且（a＞2），
    函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$，则a的值是（　　）
    A．2$\sqrt{3}$B．2+$\sqrt{3}$C．2+$\sqrt{2}$D．2$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且DE=$\frac{1}{2}$AC，连接CE、OE，连接AE交OD于点F．
    （1）求证：OE=CD；
    （2）若菱形ABCD的边长为4，∠ABC=60°，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列化简或计算正确的是（　　）
    A．$\sqrt{（-\sqrt{3}）^{2}}$=-$\sqrt{3}$B．$\sqrt{1\frac{1}{49}}$=1+$\frac{1}{7}$=$\frac{8}{7}$C．（$\sqrt{6}-\sqrt{3}$）2=9-2$\sqrt{3}$D．$\sqrt{24}$÷（-$\frac{1}{2}$$\sqrt{6}$）=-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知△ABC的三个内角、三条边长如图，则甲、乙、丙三个三角形中，和△ABC全等的图形是乙和丙．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

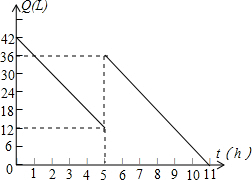    1．某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升．油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：
    （1）机动车行驶5h后加油，途中加油24升；
    （2）根据图形计算，机动车在加油前的行驶中每小时耗油多少升？
    （3）如果加油站距目的地还有400km，车速为60km/h，要到达目的地，油箱中的油是否够用？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图，已知直线AB、CD相交于O，如果∠AOC=2x°，∠BOD=（7x-100）°，则∠AOD的度数为（　　）
    A．100°B．120°C．130°D．140°

    查看答案和解析>>

    同步练习册答案