
【题目】大家喜欢玩的幻方游戏,老师精加创新改成了“幻圆”游戏,现在将-1,2,-3,4,5,6,- 7,8分别填入如图所示的四圈内,使横、整以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则![]() 的值为( )
的值为( )
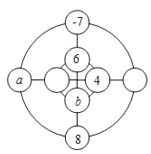
A.-8或1B.-1或1
C.-1或4D.-6或-3
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,若∠AOD=156°,OM平分∠AOB,ON平分∠BOD,∠BOD=96°,则∠MON的度数为 .
(2)如图2,若∠AOD=m°,∠NOC=23°,OM平分∠AOB,ON平分∠BOD,求∠COM的度数(用m的式子表示);
(3)如图3,若∠AOD=156°,∠BOC=22°,∠AOB=30°,OM平分∠AOC,ON平分∠BOD,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
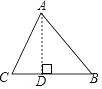
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=________;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,![]() 可以理解为
可以理解为![]() ,它表示:数轴上表示数
,它表示:数轴上表示数![]() 的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点
的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点![]() ,分别用数
,分别用数![]() 表示,那么
表示,那么![]() 两点之间的距离为
两点之间的距离为![]() ,反过来,式子
,反过来,式子![]() 的几何意义是:数轴上表示数
的几何意义是:数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离.利用此结论,回答以下问题:
的点之间的距离.利用此结论,回答以下问题:
(1)数轴上表示数8的点和表示数3的点之间的距离是_________,数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离是__________.
的点之间的距离是__________.
(2)数轴上点![]() 用数
用数![]() 表示,若
表示,若![]() ,那么
,那么![]() 的值为_________.
的值为_________.
(3)数轴上点![]() 用数
用数![]() 表示:
表示:
①若![]() ,那么
,那么![]() 的值是________.
的值是________.
②当![]() 时,数
时,数![]() 的取值范围是________,这样的整数
的取值范围是________,这样的整数![]() 有________个.
有________个.
③![]() 有最小值,最小值是___________.
有最小值,最小值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定x的一元一次方程ax=b的解为b﹣a,则称该方程是“差解方程”,例如:3x=4.5的解为4.5﹣3=1.5,则该方程3x=4.5就是“差解方程”,请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程4x=m是“差解方程”,则m=______.
(2)已知关于x的一元一次方程4x=ab+a是“差解方程”,它的解为a,则a+b=_____.
(3)已知关于x的一元一次方程4x=mn+m和﹣2x=mn+n都是“差解方程”,求代数式﹣3(m+11)+4n+2[(mn+m)2﹣m]﹣![]() [(mn+n)2﹣2n]的值.
[(mn+n)2﹣2n]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
(2)如图,AB是![]() 的直径,PA与
的直径,PA与![]() 相切于点A,OP与
相切于点A,OP与![]() 相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
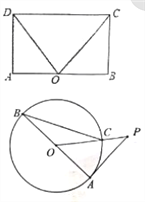
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个正方体的表面展开图,请回答下列问题:

(1)与面B、面C相对的面分别是 和 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E、F代表的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com