
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
分析 (1)设(1)班去了x人,(2)班去了y人(x<50,y>50).根据两班共去了104人且购票花费1240元,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)用1240减去团购104张票的钱数,即可得出结论.
解答 解:(1)设(1)班去了x人,(2)班去了y人.
根据题意得:$\left\{\begin{array}{l}{x+y=104}\\{13x+11y=1240}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=48}\\{y=56}\end{array}\right.$.
答:(1)班去了48人,(2)班去了56人.
(2)1240-104×9=304(元).
答:两班合作团体购票可节省304元.
点评 本题考查了二元一次方程组的应用,解题的关键是:(1)找准等量关系,列出二元一次方程组;(2)根据数量关系列式计算.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:选择题
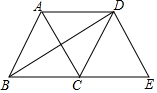 如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD=BE.其中正确的个数是( )
如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD=BE.其中正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
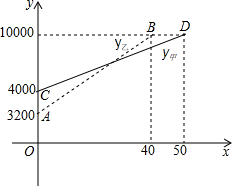 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
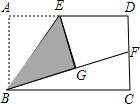 如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.
如图,在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,若DF=CF,则$\frac{AD}{AB}$的值$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
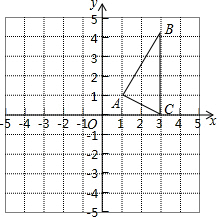 在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).
在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
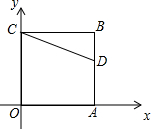 如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).
如图,正方形OABC的两边OA,OC分别在x轴上,点D(5,3)在边AB上,以C为中心,把△CDB绕点C顺时针旋转90°,则旋转后点D的对应点D′的坐标是(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com