
����Ŀ����ͼ1�������ӵ�ˮ�����ϣ���λ���ף���ȡ�����ľ���ˮλ��Ϊ0�㣬��ôͼ�е��������ݿ��Էֱ����ʲô�������С����¼�Ľ����꼾������һ����ˮλ�仯���������ĩ��ˮλ�ﵽ����ˮλ��
���� ˮλ | һ | �� | �� | �� | �� | �� | �� |
ˮλ�仯/�� | ��0.2 | ��0.8 | ��0.4 | ��0.1 | ��0.3 | ��0.4 | ��0.1 |
ʵ��ˮλ/�� | 33.6 |
ע������ʾˮλ��ǰһ������������ʾˮλ��ǰһ���½���

��1����������______������ˮλ��ߣ�ˮλ�ھ���ˮλ֮______���ϻ��£�������______������ˮλ��ͣ�ˮλ�ھ���ˮλ֮______���ϻ��£���
��2����������ȣ�����ĩ����ˮλ��______�������˻��½��ˣ���
��3����������ʵ��ˮλ��¼��
��4���Ծ���ˮλΪ0�㣬������ͳ��ͼ����ͼ2����ʾ���ܵ�ˮλ�����
���𰸡���1�������壬�ϣ�һ���ϣ���2�������ˣ���3������������4��������.
��������
��1��ȷ������ÿһ���ˮλ����Ƚ��Լ��;���ˮλ�Ƚϣ����ɵõ��𰸣�
��2�������������Ĵ�С�Ƚϣ��ɵô𰸣�
��3�������������ļӷ����ɵô𰸣�
��4��������㡢���ߣ��ɵ�����ͳ��ͼ.
�⣺��1��ȷ������ÿһ���ˮλ���ֱ������ڶ����������ˮλΪ34.4��ˮλ��ߣ�ˮλ���ھ�����33.4�����ھ���ˮλ֮�ϣ�����һ���������ˮλ33.6��ˮλ���ھ�����33.4��ˮλ�ھ���ˮλ֮�ϣ�
��2����������ˮλδ�ﵽ�����ߣ���33.4��������ˮλ33.9���ʱ���ĩ����ˮλ�������ˣ�
��3����������ʵ��ˮλ��¼��
���� ˮλ | һ | �� | �� | �� | �� | �� | �� |
ˮλ�仯/�� | ��0.2 | ��0.8 | ��0.4 | ��0.1 | ��0.3 | ��0.4 | ��0.1 |
ʵ��ˮλ/�� | 33.6 | 34.4 | 34 | 34.1 | 34.4 | 34 | 33.9 |
��4����ͼ2



 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ����ȫ��ѧ��������Ͷ����������ÿλѧ��Ͷ40���������ȡ�˲���ѧ����Ͷ������������Ƴ�����ͳ��ͼ����
��� | Ͷ������ | ���� |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
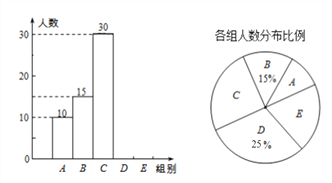
����������Ϣ����������⡣
�ٱ��γ�ȡ��ѧ������Ϊ���٣�
��ͳ�Ʊ��е�m=__________��
������ͳ��ͼ��E����ռ�İٷֱȣ�
�ܲ�ȫƵ���ֲ�ֱ��ͼ��
������ͳ��ͼ����C��������Ӧ��Բ�ĽǵĶ�����
�ޱ��α�����Ͷ����������λ��������һ����
����֪��У����900��ѧ������Ͷ����������24����Ϊ���ϸ�������Ƹ�У����Ͷ���������ϸ��ѧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ʾ����ABCD�У�BC=x��CD=y��y��x����ķ�����������ϵ��ͼ2��ʾ������ֱ��������AEF��б��EF��C�㣬MΪEF���е㣬�����н�����ȷ����

A. ��x=3ʱ��EC��EM B. ��y=9ʱ��EC��EM
C. ��x����ʱ��EC��CF��ֵ���� D. ��y����ʱ��BE��DF��ֵ���䡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ���![]() ����
����![]() ��
��![]() ��,Ȼ���ٴӣ�2��x��2�ķ�Χ��ѡȡһ�����ʵ�x������ֵ������ֵ
��,Ȼ���ٴӣ�2��x��2�ķ�Χ��ѡȡһ�����ʵ�x������ֵ������ֵ
���𰸡�4.
������������������Ƚ�ԭ��ʽ���л��⣬���������ע�ⲻΪ0���������ݲ�Ϊ0�������x��ȡֵ��Χ�ó����ʵ�x��ֵ��������뻯���Ĵ���ʽ�м��ɵó����ۣ�
���������ԭʽ= =
= =
=![]() ��
��
���� ����x�٩�1��0��1��
����x�٩�1��0��1��
���ߩ�2��x��2��xΪ��������x=2��
��x=2����![]() �еã�
�еã� ![]() =
=![]() =4��
=4��
���㣺��ʽ�Ļ�����ֵ��
�����͡������
��������
21
����Ŀ���ⷽ�̣�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
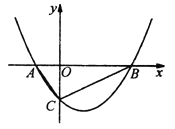
����Ŀ����ͼ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���䶥����ֱ��
���䶥����ֱ��![]() ��.
��.
��1����![]() ��ֵ;
��ֵ;
��2����![]() ���������;
���������;
��3����![]() Ϊһ���ڱ���
Ϊһ���ڱ���![]() �����
�����![]() ����
����![]() ��ĶԳƵ�
��ĶԳƵ�![]() �Ƿ��ڸ���������?
�Ƿ��ڸ���������?
��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������A��ʾ1���ֽ���A�������������ƶ�����һ�ν���A�����ƶ�3����λ���ȵ����A1����2�ν���A1����ƽ��6����λ���ȵ����A2����3�ν���A2�����ƶ�9����λ���ȵ����A3�����6���ƶ�����A6ʱ����A6�������϶�Ӧ��ʵ����_____���������ֹ����ƶ���ȥ����2017���ƶ�����A2017ʱ��A2017�������϶�Ӧ��ʵ����__________��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע��ijУ�Բ���ѧ�����ҳ���У��ȫ֪ʶ���˽�̶ȣ�����������������飬�����Ƴ���ͼ��ʾ������ͳ��ͼ![]() ������
������![]() ����ͳ��ͼ�е���Ϣ����ȫУ��2050��ѧ����������ƶ���У��ȫ��֪ʶ�ﵽ���dz��˽������������˽�����ѧ������Ϊ
����ͳ��ͼ�е���Ϣ����ȫУ��2050��ѧ����������ƶ���У��ȫ��֪ʶ�ﵽ���dz��˽������������˽�����ѧ������Ϊ![]()

A.1330B.1350C.1682D.1850
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�У���P����ABC�ڣ���Q����ABC�⣬�ҡ�ABP=��ACQ��BP=CQ��
��1����֤����ABP����ACQ.
��2���ж���APQ����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�Խ����ഹֱ���ı��ν�������ֱ�ı�������
��1�����⣺
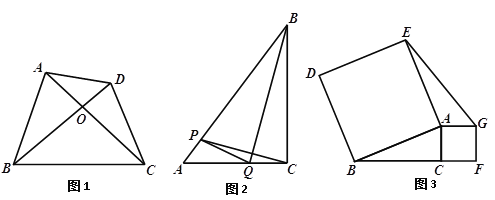
��ͼ1����֪�ı���ABCD������ֱ�ı��������Խ���AC��BD���ڵ�O��AC=8��BD=7�����ı���ABCD�����.
��2��̽����
С���� ����ֱ�ı�����ABCD����ͼ1������������̽����������һ��Աߵ�ƽ���͵�����һ��Աߵ�ƽ���ͣ���![]() ������Ϊ���ķ�����ȷ����˵��������
������Ϊ���ķ�����ȷ����˵��������
��3��Ӧ�ã�
�� ��ͼ2������ABC�У� ![]() ��AC=6��BC=8������P�ӵ�A������AB������ÿ��5����λ���ٶ����B�����˶���ͬʱ����Q�ӵ�C������CA������ÿ��6����λ���ٶ����A�����˶����˶�ʱ��Ϊt�루
��AC=6��BC=8������P�ӵ�A������AB������ÿ��5����λ���ٶ����B�����˶���ͬʱ����Q�ӵ�C������CA������ÿ��6����λ���ٶ����A�����˶����˶�ʱ��Ϊt�루![]() ��������CP��BQ��PQ�����ı���BCQP������ֱ�ı�����ʱ����t��ֵ��
��������CP��BQ��PQ�����ı���BCQP������ֱ�ı�����ʱ����t��ֵ��
�� ��ͼ3������ABC�У�![]() ��AB=3AC���ֱ���AB��ACΪ��������������ABDE��������ACFG������EG����ֱ��д���߶�EG��BC֮���������ϵ��
��AB=3AC���ֱ���AB��ACΪ��������������ABDE��������ACFG������EG����ֱ��д���߶�EG��BC֮���������ϵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com