
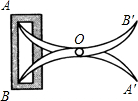
 如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..
如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等.. 分析 由O是AA′、BB′的中点,可得AO=A′O,BO=B′O,再有∠AOA′=∠BOB′,可以根据全等三角形的判定方法SAS,判定△OAB≌△OA′B′,根据全等三角形的性质即可得到结论.
解答 解:∵O是AA′、BB′的中点,
∴AO=A′O,BO=B′O,
在△OAB和△OA′B′中$\left\{\begin{array}{l}{AO=A′O}\\{∠AOA′=∠BOB′}\\{BO=B′O}\end{array}\right.$,
∴△OAB≌△OA′B′(SAS),
∴AB=A′B′,
故两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等.
故答案为:两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等.
点评 此题主要全等三角形的应用,关键是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL,要证明两个三角形全等,必须有对应边相等这一条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 甲(件) | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙(件) | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
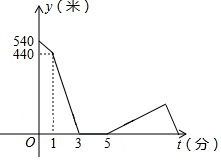 “欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.
“欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com