
【题目】已知一次函数y=(2m-3)x+m+2.
(1)若函数图像过原点,求m的值;
(2)若函数图像过点(-1,0),求m的值;
(3)若函数图像平行于直线y=-x+2求m的值;
(4)若函数图像经过第一、二、四象限,求m的取值范围.
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC, ![]() ,AD=6,BC=8,
,AD=6,BC=8, ![]() ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).

(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积.
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,在两次转弯后,仍在原来的方向上平行前进,那么这两次转弯的角度可以是( )
A. 先右转80o,再左转100 oB. 先左转80 o ,再右转80 o
C. 先左转80 o ,再左转100 oD. 先右转80 o,再右转80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣ ![]() ,y2)、点C(
,y2)、点C( ![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( ) 
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y与x的函数解析式;
(2)每分进水、出水各多少升?
(3)第 分钟时该容器内的水恰好为10升.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
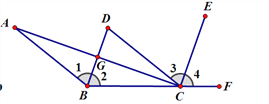
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放一矩形OABC,AB=2,OA=1,现将矩形OABC沿x轴的正方向无滑动翻转,每次翻转90°,连续翻转2019次,点B的落点依次为B1,B2,B3,B4…,则B2019的坐标为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数﹣2016将与圆周上的哪个数字重合( ) 
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全,小明骑单车上学,当他骑了一段时,想起要买文具,于是又折回到刚经过的文具店,买到文具后继续去学校,下图是他本次所用的时间与离家路程的关系示意图,根据图中提供的信息回答下列问题:

(1)小明家到学校的路程是___________米;小明在文具店停留了__________分钟.
(2)本次上学途中,小明一共行驶了多少米?
(3)我们认为骑单车的速度超过300米/分钟就超越了安全限度,问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com