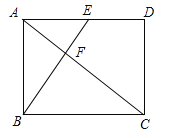
【题目】（2017山东省莱芜市）如图，在矩形ABCD中，BE⊥AC分别交AC、AD于点F、E，若AD=1，AB=CF，则AE=______．
【答案】
．
【解析】解：∵四边形ABCD是矩形，∴BC=AD=1，∠BAF=∠ABC=90°，∴∠ABE+∠CBF=90°，∵BE⊥AC，∴∠BFC=90°，∴∠BCF+∠CBF=90°，∴∠ABE=∠FCB，在△ABE和△FCB中，∵∠EAB=∠BFC=90°，AB=CF，∠ABE=∠FCB，∴△ABE≌△FCB，∴BF=AE，BE=BC=1，∵BE⊥AC，∴∠BAF+∠ABF=90°，∵∠ABF+∠AEB=90°，∴∠BAF=∠AEB，∵∠BAE=∠AFB，∴△ABE∽△FBA，∴
，∴
，∴AE=BF=AB2，在Rt△ABE中，BE=1，根据勾股定理得，AB2+AE2=BE2=1，∴AE+AE2=1，∵AE＞0，∴AE=．故答案为：．
步步高达标卷系列答案科目：初中数学 来源： 题型：
【题目】类比探究：
（1）如图1，等边△ABC内有一点P，若AP＝8，BP＝15，CP＝17，求∠APB的大小；（提示：将△ABP绕顶点A旋转到△ACP′处）
（2）如图2，在△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点，且∠EAF＝45°．求证：EF2＝BE2+FC2；
（3）如图3，在△ABC中，∠C＝90°，∠ABC＝30°，点O为△ABC内一点，连接AO、BO、CO，且∠AOC＝∠COB＝∠BOA＝120°，若AC＝1，求OA+OB+OC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】给出下面四个命题，其中真命题的个数有（ ）
(1)平分弦的直径垂直于这条弦，并且平分这条弦所对的弧；
(2)90°的圆周角所对的弦是直径；
(3)在同圆或等圆中，圆心角的度数是圆周角的度数的两倍；
(4)如下图，顺次连接圆的任意两条直径的端点，所得的四边形一定是矩形．
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如下（注：水费按月份结算，表示立方米）
请根据上表的内容解答下列问题：
（1）填空：若该户居民2月份用水5m3，则应交水费 元；3月份用水8m3，则应收水费 元；
（2）若该户居民4月份用水am3（其中a＞10m3），则应交水费多少元（用含a的代数式表示，并化简）？
（3）若该户居民5、6两个月共用水14m3（6月份用水量超过了5月份），设5月份用水xm3，直接写出该户居民5、6两个月共交水费多少元（用含x的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛，他收集了小明、小白近期10次数学考试成绩，并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70，100 | 85 | 100 |
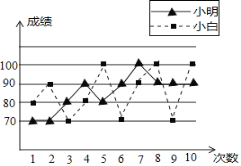
(1)根据折线统计图，张老师绘制了不完整的统计表，请你补充完整统计表；
(2)你认为张老师会选择哪位同学参加比赛？并说明你的理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过
上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．
（1）求证：△ECF∽△GCE；
（2）求证：EG是⊙O的切线；
（3）延长AB交GE的延长线于点M，若tanG=
，AH=3
，求EM的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为直线AB上一点，∠DOC为直角，OE平分∠BOC，OF平分∠AOD，OG平分∠AOC，下列结论：①∠BOE与∠DOF互为余角；②2∠AOE﹣∠BOD＝90°；③∠EOD与∠COG互为补角；④∠BOE﹣∠DOF＝45°；其中正确的是（ ）
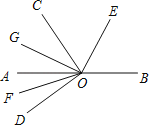
A.①②③④B.③④C.②③D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
