
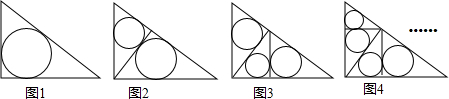
| A. | 4π | B. | 3π | C. | 2π | D. | π |
分析 先找出计算直角三角形内切圆半径的规律:半径r=$\frac{a+b+c}{2}$,长特殊到一般,探究规律后,利用规律即可解决问题.
解答 解:图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F,则∠OEC=∠OFC=90°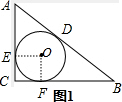
∵∠C=90°
∴四边形OECF为矩形
∵OE=OF
∴矩形OECF为正方形
设圆O的半径为r,则OE=OF=r,AD=AE=3-r,BD=4-r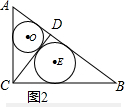
∴3-r+4-r=5,r=$\frac{3+4-5}{2}$=1
∴S1=π×12=π
图2,由S△ABC=$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×CD
∴CD=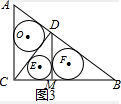 $\frac{12}{5}$由勾股定理得:AD=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,BD=5-$\frac{9}{5}$=$\frac{16}{5}$,
$\frac{12}{5}$由勾股定理得:AD=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,BD=5-$\frac{9}{5}$=$\frac{16}{5}$,
由(1)得:
⊙O的半径=$\frac{\frac{9}{5}+\frac{12}{5}-3}{2}$=$\frac{3}{5}$,⊙E的半径=$\frac{\frac{12}{5}+\frac{16}{5}-4}{2}$=$\frac{4}{5}$,
∴S1+S2=π×( $\frac{3}{5}$)2+π×( $\frac{4}{5}$)2=π.
图3,由S△CDB=$\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$=$\frac{1}{2}$×4×MD
∴MD=$\frac{48}{25}$,
由勾股定理得:CM=$\sqrt{(\frac{12}{5})^{2}-(\frac{48}{25})^{2}}$=$\frac{36}{25}$,MB=4-$\frac{36}{25}$=$\frac{64}{25}$,
由(1)得:⊙O的半径=$\frac{3}{5}$,:⊙E的半径=$\frac{\frac{48}{25}+\frac{36}{25}-\frac{12}{5}}{2}$=$\frac{12}{25}$,
∴⊙F的半径=$\frac{\frac{48}{25}+\frac{64}{25}-\frac{12}{5}}{2}$=$\frac{16}{25}$,
∴S1+S2+S3=π×( $\frac{3}{5}$)2+π×( $\frac{12}{25}$)2+π×( $\frac{16}{25}$)2=π
…
观察规律可知S1+S2+S3+…+S6=π.
故选D.
点评 本题考查了直角三角形的内切圆,这是一个图形变化类的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解;解决此题的思路为:①先找出计算直角三角形内切圆半径的规律:半径r=$\frac{a+b-c}{2}$(a、b是直角边,c为斜边);②利用面积相等计算斜边上的高;③运用勾股定理计算直角三角形的边长.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x}-\frac{1}{y}=\frac{x-y}{xy}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | C. | $\frac{-a-1}{{{a^2}-1}}=-\frac{1}{a+1}$ | D. | $\frac{{{a^2}-1}}{a}•\frac{1}{a+1}=-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
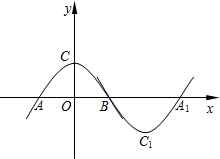 如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1
如图所示,抛物线l1:y=ax2+b(a<0,b>0)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,将抛物线l1绕点B旋转180°,得到新的抛物线l2,它的顶点为C1,与x轴的另一个交点为A1查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
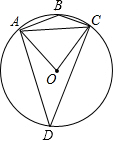 如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )| A. | 30° | B. | 50° | C. | 40° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
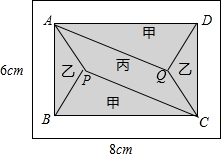 小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3(x-3)2-3 | B. | y=3x2 | C. | y=3(x+3)2-3 | D. | y=3x2-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com